Расчет площади неправильных фигур: данные из таблиц Tehtab.ru
Как посчитать площадь стен для укладки плитки?
Для того чтобы посчитать площадь стен для укладки плитки, необходимо измерить высоту и длину каждой стены, которую вы собираетесь покрыть плиткой. Затем нужно умножить длину на высоту каждой стены, чтобы получить площадь поверхности стены.
Далее, нужно сложить площади всех стен вместе, чтобы получить общую площадь стен, которую необходимо покрыть плиткой. При этом необходимо учесть площадь дверных и оконных проемов, если они есть. Для этого, нужно измерить ширину и высоту каждого проема, а затем вычесть площадь проема из общей площади стены.
Таким образом, формула для подсчета площади стен для укладки плитки будет выглядеть следующим образом:
Площадь стены = длина стены x высота стены Общая площадь стен = сумма площадей всех стен — сумма площадей проемов (дверей, окон и т.д.)
После того, как вы подсчитали общую площадь стен, необходимо добавить к этому значению еще некоторое количество плитки, которое понадобится на резку и запасы. Как правило, рекомендуется добавить от 10% до 20% от общей площади стен в качестве запаса на резку и непредвиденные расходы.
|
Площади неправильных фигур. Определение площади неправильных плоских образований возможно приблизительно с помощью инструментов, таких как планиметр, формула трапеции, правило средних ординат и формула Симпсона. Эти методы могут быть использованы в различных областях, например, инженерами для расчета площади индикаторных диаграмм паровых двигателей, землемерами для оценки площадей участков, а также кораблестроителями для вычисления горизонтальных или поперечных сечений кораблей. Если интересует вопрос о том, как выполнить подсчет площади неправильной фигуры, то указанные методы предоставляют соответствующие решения. Подобные методы могут быть использованы, например, инженерами для оценки площадей индикаторных диаграмм паровых двигателей, землемерами для оценки площадей земельных участков, кораблестроителями для оценки горизонтальных или поперечных сечений кораблей. Планиметр. Это инструмент для непосредственного измерения малых площадей, очерченных неправильной кривой. Формула трапеций.
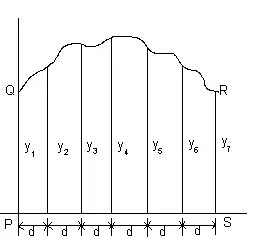
Чтобы определить площадь PQRS на рис. выше , необходимо: — Разделить PS на любое число равных интервалов шириной d каждый (чем больше количество интервалов, тем выше точность). — Аккуратно измерить ординаты у1, у2, у3 и так далее. -Площадь SPQRS = d[(у1+у7)/2 +у2+у3+ у4+у5+у6] В общем, согласно формуле трапеций: Площадь = (ширина интервала)[1/2(первая + последняя ордината)+(сумма остальных ординат)]. Правило средних ординат.
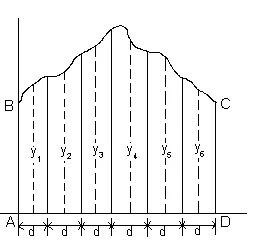
Чтобы определить площадь ABCD на рис. выше, необходимо: — Разделить основание AD на любое количество равных интервалов шириной d каждый (чем больше количество интервалов, тем выше точность). — Восстановить перпендикуляр из середины каждого интервала (на рис. выше оказаны штриховыми линиями). -Точно измерить ординаты у1, у2, у3 и так далее. — Площадь SABCD = d(у1 +у2+у3+ у4+у5+у6) В общем виде, правило средних ординат гласит: Площадь = (ширина интервала)*(сумма средних ординат). Формула Симпсона .
Чтобы определить площадь PQRS на рис.выше, необходимо: — Разделить основание PS на четное количество равных интервалов шириной d каждый (чем больше количество интервалов, тем выше точность). — Точно измерить ординаты у1, у2, у3 и так далее. — Площадь SPQRS = (d/3)*[(у1+у7) +4(у2+у4+ у6)+2(у3+у5)] В общем виде, формула Симпсона: Площадь = 1/3(ширина интервала)[(первая + последняя ордината)+4(сумма четных ординат)+2(сумма нечетных ординат)]. Пример. Определение площади под кривой с помощью формулы трапеций, правила средних ординат, формулы Симпсона.
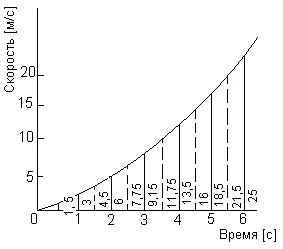
Машина стартует из состояния покоя, и ее скорость измеряется каждую секунду в течение 6 секунд:
Хотя мы понимаем что увеличение числа разбиений увеличивает точность, но для простоты решения возьмем количество разбиений, равное 7. Определить расстояние, пройденное за 6 секунд (т.е. площадь под графиком): а) по формуле трапеций, б) по правилу средних ординат, в)по формуле Симпсона. а) Формула трапеций. Время на графике делится на 6 интервалов шириной 1 с и измеряются ординаты. Итак, площадь S определяется формулой S= 1[(0+25)/2 +3+6+ 9,15+13,5+18,5]=62,65 м б) Правило средних ординат. Время на графике делится на 6 интервалов шириной 1 с. На рис. пунктирной линией показаны средние ординаты. Измерена каждая средняя ордината. Итак, площадь S определяется формулой S= 1(1,5 +4,5+7,75+11,75+16+21,5)=63 м в) Формула Симпсона . Время на графике делится на 6 интервалов шириной 1 с и измеряются ординаты. Итак, площадь S определяется формулой: S= (1/3)*[(0+25) +4(3+9,15+ 18,5)+2(6+13,5)]= 61,2 м. Т.е. машина проехала в среднем 62,283 м. |