Измерение Площади Поперечного Сечения — Расчеты с Помощью Формулы
Что значит поперечное сечение
Прежде чем перейти к более детальному изложению основной концепции, необходимо декодировать значение данного термина и разобраться в различиях между проводом и кабелем. Провод — это проводник, который используется для объединения различных участков электрической цепи. Чтобы лучше понять этот процесс, можно прибегнуть к формуле поперечного сечения.

Первые используются в воздушных линиях электрических передач. Вторые применяются в электрических устройствах, щитках или шкафах. В быту они находятся внутри электрической проводки.
К сведению! Изолированные и одножильные проводники используются везде, а многожильные применяются там, где нужны изгибы с малым радиусом.
Поперечным сечением называется фигура, которая образуется от проводникового рассечения плоскостью направления. Площадь, которая получена при перпендикулярном разрезе любого вида провода, указывается в квадратных миллиметрах. Это важный параметр для расчета электрической сети.
Шар и сфера, их сечения
Напомним, что шаром
называется тело, состоящее из всех точек пространства, находящихся на расстоянии не большем заданного от некоторой данной точки. Эта точка –
центр
шара, а заданное расстояние –
радиус
шара.
Шар так же, как цилиндр и конус, является телом вращения. Он получается в результате вращения полукруга вокруг его диаметра.
Поверхность, образуемая при этом вращении полуокружности, называется сферой
. Можно сказать, что сфера – это как бы оболочка, или граница, шара. Как окружность есть граница круга, так и сфера – это граница шара.
Назовём элементы сферы и шара.
Радиус
сферы – это отрезок, соединяющий центр сферы и любую её точку.
Хорда
сферы – отрезок, соединяющий две точки сферы.
Диаметр
сферы – хорда сферы, проходящая через её центр.
Радиус, хорда, диаметр шара – это радиус, хорда, диаметр его сферы.
Любое сечение шара плоскостью есть круг. Центром этого круга является основание перпендикуляра, опущенного из центра шара на секущую плоскость.
Плоскость, которая проходит через центр шара, называется диаметральной плоскостью
. Сечение ею шара –
большим кругом
, а сечение сферы –
большой окружностью
.
Любая диаметральная плоскость шара является его плоскостью симметрии
. Центр шара является его
центром симметрии
.
Плоскость, проходящая через точку А
сферы и перпендикулярно радиусу, проведённому в эту точку, называется
касательной плоскостью
. Точка
А
называется
точкой касания
.
Свойство касательной плоскости к сфере
: радиус сферы, проведённый в точку касания, перпендикулярен касательной плоскости.
Признак касательной плоскости к сфере
: плоскость, перпендикулярная радиусу сферы в конечной его точке на сфере, является касательной к сфере.
Касательная плоскость пересекается с шаром в единственной точке – в точке касания.
Касательной прямой
к сфере (шару) называется прямая, имеющая со сферой единственную общую точку.
Отрезки касательных к сфере, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр сферы.
Линией пересечения двух сфер является окружность.
Площадь сферы
радиуса : .
Объём шара
радиуса : .
Шаровым сегментом
называется часть шара, отсекаемая от него плоскостью.
Площадь боковой поверхности шарового сегмента:
.
Объём шарового сегмента:
,
где – радиус шара, – высота шарового сегмента.
Шаровым сектором
называется тело, которое получается из шарового сегмента и конуса, основанием которого является сечение плоскостью данного шара.
Площадь боковой поверхности шарового сектора:
.
Объём шарового сектора
:
,
где – радиус шара, – высота сегмента.
Шар называется вписанным в многогранник
, а многогранник –
описанным около шара
, если поверхность шара касается всех граней многогранника.
Шар называется описанным около многогранника
, а многогранник –
вписанным в шар
, если поверхность шара проходит через все вершины многогранника.
Шар называется вписанным в цилиндр
, а цилиндр –
описанным около шара
, если поверхность шара касается оснований цилиндра и всех образующих.
Шар называется описанным около цилиндра
, если окружности оснований цилиндра принадлежат поверхности шара.
Шар называется вписанным в конус
(усечённый конус)
, а конус (усечённый конус) –
описанным около шара
, если поверхность шара касается основания (оснований) конуса и всех образующих.

Шар называется описанным около конуса (усечённого конуса)
, если окружность основания и вершина (окружности оснований) конуса принадлежат поверхности шара.
Если боковые грани пирамиды одинаково наклонены к плоскости основания, то в такую пирамиду можно вписать
шар.
Около пирамиды можно описать шар тогда и только тогда, когда около её основания можно описать окружность.
Если боковые рёбра пирамиды равны между собой (или одинаково наклонены к плоскости основания), то около такой пирамиды можно описать шар.
В призму можно вписать
шар тогда и только тогда, когда в перпендикулярное сечение этой призмы можно вписать окружность, а высота призмы равна диаметру окружности, вписанной в это перпендикулярное сечение.
Описать
шар около призмы можно тогда и только тогда, когда призма прямая и около её основания можно описать окружность.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задача первая. Радиус шара увеличили в раза. Во сколько раз увеличился объём шара?
Решение.

Задача вторая. Объём шара равен см3. Найдите диаметр шара.
Решение.

Задача третья. Шар пересечен плоскостью. Площадь сечения равна см2. Расстояние от центра шара до плоскости сечения равно см. Найдите площадь поверхности шара.
Решение.

Задача четвёртая. В конус с радиусом основания, равным см, и высотой, равной см, вписан шар. Найдите отношение площади боковой поверхности конуса к площади поверхности шара.
Решение.
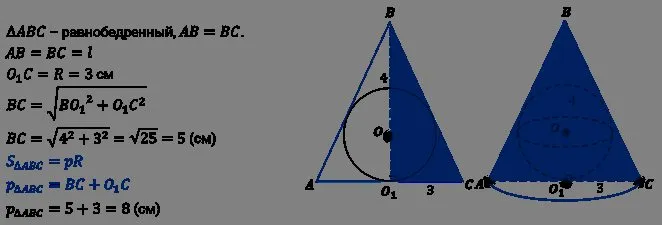
Задача пятая. Найдите объём шарового сектора, если радиус окружности его основания равен см, а радиус шара – см.
Решение.

Задача шестая. Шар с радиусом см пересечён плоскостью, находящейся на расстоянии см от центра шара. Найдите площадь сечения.
Решение.

Сфера применения
Поперечное сечение на чертеже изображено в виде фигуры, которая образована делением детали плоскостью. Используется в электротехнике, электричестве, когда рассматривается проводниковая жила под прямым углом к его продольной половине. Через поделенную жилу проходят электроны.
Обратите внимание! Диаметр жилы — это не сечение. Для определения площади жилы нужно использовать специальную формулу определения круга.
Зная, какая величина разреза провода, длина и удельное сопротивление, можно узнать, какое имеет сопротивление проводник электротоку, проходящий сквозь его структуру. Если неправильно подобрать разрез проводника, это может привести к возгоранию электрической проводки в системе в результате его перегрева, оплавления.
Вам это будет интересно Особенности переходного сопротивления
Целью расчета площади поперечного сечения может быть получение нужного количества электроэнергии для нормальной работы электрических приборов, исключение переплат неиспользуемым энергоносителем, подключение мощной техники к сетевому напряжению, предотвращение возгорания участка, исключение оплавки слоя изоляции, предотвращение появления короткого замыкания в бытовой и промышленной сетях. Также это может быть получение правильной организации системы освещения.
К сведению! Нормальным сечением проводника для освещения является показатель 1,5 мм² для линии и 4-6 мм² для ввода.
Таблица диаметров и сечения проводов
Формула для расчёта диаметра достаточно проста и выдаёт стандартные значения для конкретного диаметра. Поэтому часто можно увидеть в продаже соответствующие таблицы площадей круга.
Вам это будет интересно Замеры освещенности помещения
Таблица соотношений диаметров и площадей проводов
Таким способом можно пользоваться в том случае, если под рукой оказался стандартный проводник, указанный в ГОСТ. Например — при диаметре сердечника 2.8 мм площадь его сечения составит 6 мм2.
Прочитав эту статью, любой человек сможет самостоятельно рассчитать площадь поперечного сечения провода или кабеля. Это пригодится при замене старой проводки или при монтаже новой кабельной линии. Главное условия подбора – повышенная точность, так как идеального соотношения качества, простоты установки, безопасности и оптимальной цены можно добиться только после проведения кропотливых замеров.
Чем можно делать расчеты поперечного сечения
Иногда приходится измерять поперечное сечение самостоятельно, поскольку на провод не нанесена маркировка. Это не повод, чтобы не использовать его. Сперва нужно выяснить, из какого материала была сделана жила. Есть белая алюминиевая, медная красная и латунная желтая. После этого необходимо рассчитать площадь. Для этого следует выяснить проводниковый диаметр, убрав изоляцию. Диаметр можно измерить, используя:
- штангенциркуль, микрометр;
- карандаш и линейку.
Важно! Во втором случае результат будет приблизительным. Его использовать следует в крайних случаях. Лучше рассчитывать диаметр по формуле и штангенциркулем.
Штангенциркуль
Сделать штангенциркулем можно замер провода, который имеет любые размеры. Для этого нужно поместить его между штангенциркульными щипцами. Сделать так, чтобы они смотрены на деление шкалы. Затем подсчитать значение.

Целые числа можно получить по верхней шкале, а десятичные — по нижней.
Карандаш + линейка
Если штангенциркуля нет, а длина оголенного проводника позволяет сделать его накрутку на карандаш длиной не меньше 1 см, можно использовать данный способ. Все, что нужно – подсчитать витки, которые поместились на отрезке длины 1 см. Диаметр получается делением длины отрезка на витки.

Обратите внимание! Точность измерения будет зависеть от того, как плотно была сделана намотка, и какая у нее длина.
В чем измеряется поперечное сечение
После определения диаметра указанными способами площадь сечения можно определить по формуле или специальной таблице. Измеряется она в квадратных миллиметрах. Данная единица измерения производная согласно единой международной системе измерений.
Вам это будет интересно Чет отличается RJ-11 от RJ-12
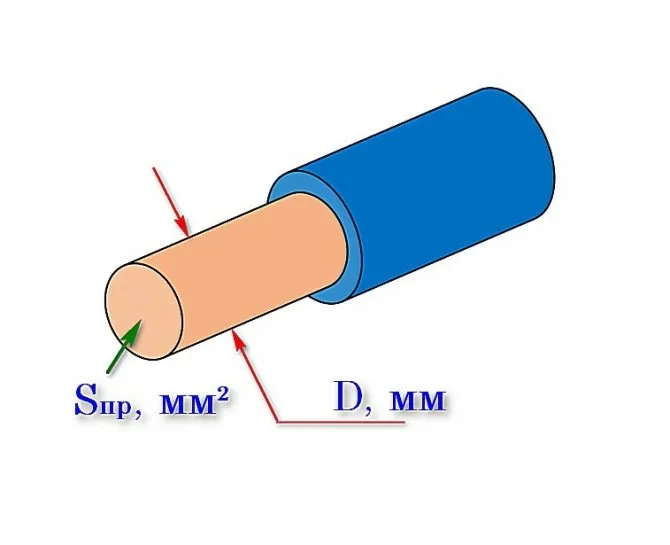
При этом разрез жил всегда круглый.
Формула измерения площади поперечного сечения
Рассчитать поперечное сечение, а именно площадь можно через формулу круга S = π * R2, где первым звеном является площадь круга, вторым — константа Пи 3,14, а третьим — радиус. Принимая во внимание тот факт, что радиус является одной второй диаметра, то формула может быть преобразована по желанию. Рассчитывая площадь, следует использовать диаметр.
Обратите внимание! Чтобы определить сечение многожильного провода, нужно вычислить площадь одной жилы, а затем полученное значение перемножить на количество проводниковых жил.
Определяя диаметр проводника комнатной электропроводки, нужно взять во внимание показатель одновременной максимальной потребительской нагрузки. Принимая в расчет показатель мощности, берется сечение линий, идущих от центра счетчика и вводных автоматов к распределительной коробке. Это места с суммарной нагрузкой всех подсоединенных потребителей. Делать выбор лучше в пользу медного провода с жилами не меньше 6 мм².

Поперечным сечением называется площадь среза под углом 90° к оси. Рассчитывать его на проводнике можно штангенциркулем, карандашом, линейкой. Измеряется оно в квадратных миллиметрах. Подсчитывается по специальной формуле, представленной выше. Ничего сложного в этом нет, главное — выбрать самый точный вариант.
Важные измерения
Радиус (обозначается r) — единственное необходимое измерение. Это расстояние от любой точки на поверхности сферы до её центра. Самый длинный отрезок, равный двум r, называется диаметром (d). Земля называется сфероидом, потому что она очень близка к шару, но не идеально круглая. Она немного вытянута на северном и южном полюсах.

Впервые вычислить площадь (S) поверхности шара удалось Архимеду. Именно он установил, что для того, чтобы найти S любого трёхмерного объекта, необходимо измерить его радиус. Для сферы получилась следующая формула: S = 4 * π * r ². Для того чтобы понять, как это работает, следует рассмотреть пример. Известно, что радиус детского мяча 10 см. Остаётся ещё одна неизвестная — число π. Это математическая константа, которая выражает отношение длины окружности к её диаметру и равна примерно 3,14. Далее, следует подставить цифры в уравнение:
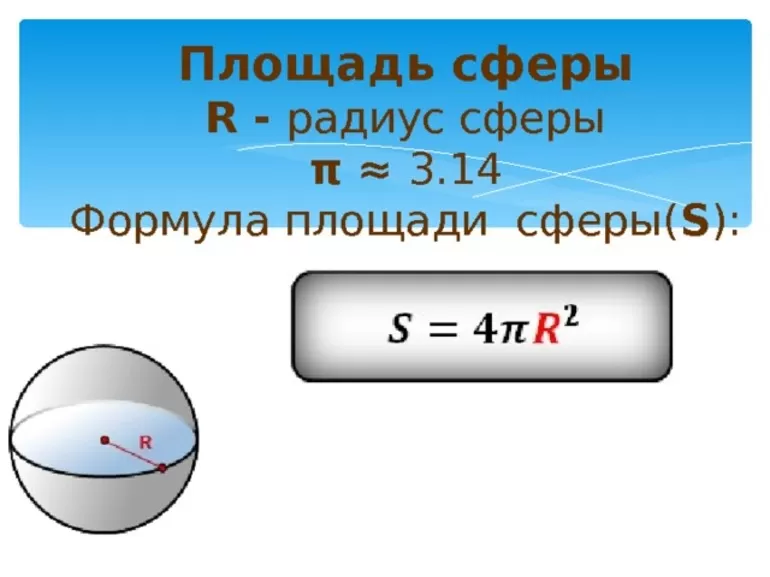
- S = 4 * 3,14 * 10²;
- S мяча равна ≈ 1256 см².
Таким образом, можно найти площадь сферы через её радиус по формуле, полученной ещё в античности. Ещё одна важная характеристика — это объём (V) фигуры. Он вычисляется следующим образом: V = (4/3) * π * r³. Если придерживаться условий задачи, то V мяча = (4/3) * 3,14 * 10³ равен ≈ 4187 см ³. Сейчас можно избежать длительных расчётов, если нужно узнать площадь сферы, онлайн-калькуляторы — сервисы, которые очень в этом помогают.
Сектор сферы — это слой между двумя правильными круговыми конусами, имеющими общую вершину в центре шара и общую ось.
Надо сказать, что внутренний конус может иметь основание с нулевым радиусом. Формула, по которой определяют площадь сектора, следующая: S = 2 * π * r * h, где h — высота. К слову, эта же формула применима, если необходимо найти S части шара, отрезанной плоскостью, то есть полусферы. Такая же формула применяется при нахождении S сегмента (часть между двумя параллельными плоскостями) и зоны сферы (изогнутая поверхность сферического сегмента).
Какие сечения проводов есть?
Сечение провода — это площадь проводника, который проходит электрический ток. Различные типы проводов имеют различные сечения, которые определяются их электрическими характеристиками, включая проводимость, напряжение и теплопроводность.
Некоторые из самых распространенных сечений проводов:
- Сечение провода в мм2: 0,5, 0,75, 1, 1,5, 2,25, 4, 6, 10, 16, 25, 35, 50, 70, 95, 120, 150 и т.д.
- Сечение провода в AWG (American Wire Gauge): 20, 18, 16, 14, 12, 10, 8 и т.д.
Выбор сечения провода зависит от многих факторов, включая мощность электрической нагрузки, длину провода и электрические характеристики провода. Важно выбрать правильное сечение провода, чтобы избежать перегрева или перегрузки электрической системы.