СП 52-101-2003

Текущий кодекс правил содержит указания по расчету и планированию железобетонных и бетонных конструкций для промышленных и гражданских зданий и сооружений из тяжелого бетона без предварительного напряжения арматуры, согласно требованиям СНиП 52-01-03 «Бетонные и железобетонные конструкции. Основные положения».

Система нормативных документов в строительстве

СВОД ПРАВИЛ ПО ПРОЕКТИРОВАНИЮ И СТРОИТЕЛЬСТВУ

БЕТОННЫЕ И ЖЕЛЕЗОБЕТОННЫЕ КОНСТРУКЦИИ БЕЗ ПРЕДВАРИТЕЛЬНОГО НАПРЯЖЕНИЯ АРМАТУРЫ

CONCRETE AND REINFORCED CONCRETE STRUCTURES WITHOUT PRESTRESSING

СП 52-101-2003

УДК 624.012.3/.4(083.13)

Дата введения 2004-03-01

ПРЕДИСЛОВИЕ

1 РАЗРАБОТАН Научно-исследовательским, проектно-конструкторским и технологическим институтом бетона и железобетона (ГУП «НИИЖБ») Госстроя России

ВНЕСЕН Управлением технического нормирования, стандартизации и сертификации в строительстве и ЖКХ Госстроя России

2 ОДОБРЕН для применения постановлением Госстроя России от 25.12.2003 № 215

3 ВВЕДЕН ВПЕРВЫЕ

ВВЕДЕНИЕ

Решение вопроса о применении Свода правил при проектировании бетонных и железобетонных конструкций конкретных зданий и сооружений относится к компетенции заказчика или проектной организации. В случае если принято решение о применении настоящего Свода правил, должны быть выполнены все установленные в нем требования.

Приведенные в Своде правил единицы физических величин выражены: силы — в ньютонах (Н) или в килоньютонах (кН); линейные размеры — в мм (для сечений) или в м (для элементов или их участков); напряжения, сопротивления, модули упругости — в мегапаскалях (МПа); распределенные нагрузки и усилия — в кН/м или Н/мм.

Свод правил разработали д-ра техн. наук А.С. Залесов, А.И. Звездов, Т.А. Мухамедиев, Е.А. Чистяков (ГУП «НИИЖБ» Госстроя России).

1 ОБЛАСТЬ ПРИМЕНЕНИЯ

Настоящий Свод правил распространяется на проектирование бетонных и железобетонных конструкций зданий и сооружений различного назначения, выполненных из тяжелого бетона классов по прочности на сжатие от В10 до В60 без предварительного напряжения арматуры и эксплуатируемых в климатических условиях России, в среде с неагрессивной степенью воздействия, при статическом действии нагрузки.

Свод правил не распространяется на проектирование бетонных и железобетонных конструкций гидротехнических сооружений, мостов, покрытий автомобильных дорог и аэродромов и других специальных сооружений.

2 НОРМАТИВНЫЕ ССЫЛКИ

В настоящем Своде правил использованы ссылки на следующие нормативные документы:

СНиП 52-01-2003 Бетонные и железобетонные конструкции. Основные положения

СНиП 2.01.07-85* Нагрузки и воздействия

СНиП 23-01-99* Строительная климатология

ГОСТ 13015.0—2003 Конструкции и изделия бетонные и железобетонные сборные. Общие технические требования

ГОСТ 14098—91 Соединения сварные арматуры и закладных изделий железобетонных конструкций. Типы, конструкции и размеры

3 ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ

В настоящем Своде правил использованы термины по СНиП 52-01 и другим нормативным документам, на которые имеются ссылки в тексте.

4 ОБЩИЕ УКАЗАНИЯ

4.1 ОСНОВНЫЕ ПОЛОЖЕНИЯ

4.1.1 Бетонные и железобетонные конструкции должны быть обеспечены с требуемой надежностью от возникновения всех видов предельных состояний расчетом, выбором показателей качества материалов, назначением размеров и конструированием согласно указаниям настоящего Свода правил. При этом должны быть выполнены технологические требования при изготовлении конструкций и соблюдены требования по эксплуатации зданий и сооружений, а также требования по экологии, устанавливаемые соответствующими нормативными документами.

4.1.2 Конструкции рассматривают как бетонные, если их прочность обеспечена одним только бетоном.

Бетонные элементы применяют:

а) преимущественно на сжатие при расположении продольной сжимающей силы в пределах поперечного сечения элемента;

б) в отдельных случаях в конструкциях, работающих на сжатие, при расположении продольной сжимающей силы за пределами поперечного сечения элемента, а также в изгибаемых конструкциях, когда их разрушение не представляет непосредственной опасности для жизни людей и сохранности оборудования и когда применение бетонных конструкций целесообразно.

4.2 ОСНОВНЫЕ РАСЧЕТНЫЕ ТРЕБОВАНИЯ

4.2.1 Расчеты бетонных и железобетонных конструкций следует производить по предельным состояниям, включающим:

— предельные состояния первой группы (по полной непригодности к эксплуатации вследствие потери несущей способности);

— предельные состояния второй группы (по непригодности к нормальной эксплуатации вследствие образования или чрезмерного раскрытия трещин, появления недопустимых деформаций и др.).

Расчеты по предельным состояниям первой группы, содержащиеся в настоящем СП, включают расчет по прочности с учетом в необходимых случаях деформированного состояния конструкции перед разрушением.

Расчеты по предельным состояниям второй группы, содержащиеся в настоящем СП, включают расчеты по раскрытию трещин и по деформациям.

4.2.2 Расчет по предельным состояниям конструкции в целом, а также отдельных ее элементов следует, как правило, производить для всех стадий: изготовления, транспортирования, возведения и эксплуатации; при этом расчетные схемы должны отвечать принятым конструктивным решениям.

4.2.3 Расчеты железобетонных конструкций необходимо, как правило, производить с учетом возможного образования трещин и неупругих деформаций в бетоне и арматуре.

Определение усилий и деформаций от различных воздействий в конструкциях и в образуемых ими системах зданий и сооружений следует производить по методам строительной механики, как правило, с учетом физической и геометрической нелинейности работы конструкций.

4.2.4 При проектировании бетонных и железобетонных конструкций надежность конструкций устанавливают расчетом путем использования расчетных значений нагрузок и воздействий, расчетных значений характеристик материалов, определяемых с помощью соответствующих частных коэффициентов надежности по нормативным значениям этих характеристик с учетом степени ответственности зданий и сооружений.

Нормативные значения нагрузок и воздействий, коэффициентов сочетаний, коэффициентов надежности по нагрузке, коэффициентов надежности по назначению конструкций, а также подразделение нагрузок на постоянные и временные (длительные и кратковременные) принимают согласно СНиП 2.01.07.

4.2.5 При расчете элементов сборных конструкций на воздействие усилий, возникающих при их подъеме, транспортировании и монтаже, нагрузку от веса элементов следует принимать с коэффициентом динамичности, равным: 1,60 — при транспортировании, 1,40 — при подъеме и монтаже. Допускается принимать более низкие, обоснованные в установленном порядке, значения коэффициента динамичности, но не ниже 1,25.

4.2.6 При расчете по прочности бетонных и железобетонных элементов на действие сжимающей продольной силы следует учитывать случайный эксцентриситет е_a, принимаемый не менее:

¹/₆₀₀ длины элемента или расстояния между его сечениями, закрепленными от смещения;

¹/₃₀ высоты сечения;

10 мм.

Для элементов статически неопределимых конструкций значение эксцентриситета продольной силы относительно центра тяжести приведенного сечения е₀ принимают равным значению эксцентриситета, полученного из статического расчета, но не менее е₀.

Для элементов статически определимых конструкций эксцентриситет е₀ принимают равным сумме эксцентриситетов — из статического расчета конструкций и случайного.

5 МАТЕРИАЛЫ ДЛЯ БЕТОННЫХ И ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ

5.1 БЕТОН

Показатели качества бетона и их применение при проектировании

5.1.1 Для бетонных и железобетонных конструкций, проектируемых в соответствии с требованиями настоящего Свода правил, следует предусматривать конструкционный тяжелый бетон средней плотности от 2200 кг/м³ до 2500 кг/м³ включительно.

5.1.2 Основными показателями качества бетона, устанавливаемыми при проектировании, являются:

а) класс бетона по прочности на сжатие В;

б) класс по прочности на осевое растяжение В_t (назначают в случаях, когда эта характеристика имеет главенствующее значение и ее контролируют на производстве);

в) марка по морозостойкости F (назначают для конструкций, подвергаемых действию попеременного замораживания и оттаивания);

г) марка по водонепроницаемости W (назначают для конструкций, к которым предъявляют требования ограничения водопроницаемости).

Классы бетона по прочности на сжатие В и осевое растяжение В_t отвечают значению гарантированной прочности бетона, МПа, с обеспеченностью 0,95.

5.1.3 Для бетонных и железобетонных конструкций следует предусматривать бетоны следующих классов и марок:

а) классов по прочности на сжатие:

В10; В15; В20; В25; В30; В35; В40; В45; В50; В55; В60;

б) классов по прочности на осевое растяжение:

В_t0,8; В_t1,2; В_t1,6; В_t2,0; В_t2,4; В_t2,8; В_t3,2;

в) марок по морозостойкости:

F50; F75; F100; F150; F200; F300; F400; F500;

г) марок по водонепроницаемости:

W2; W4; W6; W8; W10; W12.

5.1.4 Возраст бетона, отвечающий его классу по прочности на сжатие и осевое растяжение (проектный возраст), назначают при проектировании исходя из возможных реальных сроков загружения конструкций проектными нагрузками. При отсутствии этих данных класс бетона устанавливают в возрасте 28 сут.

Значение отпускной прочности бетона в элементах сборных конструкций следует назначать в соответствии с ГОСТ 13015.0 и стандартами на конструкции конкретных видов.

5.1.5 Для железобетонных конструкций рекомендуется применять класс бетона по прочности на сжатие не ниже В15.

5.1.6 Марку бетона по морозостойкости назначают в зависимости от требований, предъявляемых к конструкциям, режима их эксплуатации и условий окружающей среды.

Для надземных конструкций, подвергаемых атмосферным воздействиям окружающей среды при расчетной отрицательной температуре наружного воздуха в холодный период от минус 5 °С до минус 40 °С, принимают марку бетона по морозостойкости не ниже F75, а при расчетной температуре наружного воздуха выше минус 5 °С в указанных выше конструкциях марку бетона по морозостойкости не нормируют.

В остальных случаях требуемые марки бетона по морозостойкости устанавливают в зависимости от назначения конструкций и условий окружающей среды по специальным указаниям.

5.1.7 Марку бетона по водонепроницаемости назначают в зависимости от требований, предъявляемых к конструкциям, режима их эксплуатации и условий окружающей среды.

Для надземных конструкций, подвергаемых атмосферным воздействиям при расчетной отрицательной температуре наружного воздуха выше минус 40 °С, а также для наружных стен отапливаемых зданий марку бетона по водонепроницаемости не нормируют.

В остальных случаях требуемые марки бетона по водонепроницаемости устанавливают по специальным указаниям.

Нормативные и расчетные значения характеристик бетона

Нормативные значения прочностных характеристик бетона

5.1.8 Основными прочностными характеристиками бетона являются нормативные значения:

— сопротивления бетона осевому сжатию R_b,n;

— сопротивления бетона осевому растяжению R_bt,n;

Нормативные значения сопротивления бетона осевому сжатию (призменная прочность) и осевому растяжению (при назначении класса бетона по прочности на сжатие) принимают в зависимости от класса бетона по прочности на сжатие В согласно таблице 5.1.

При назначении класса бетона по прочности на осевое растяжение В_t нормативные значения сопротивления бетона осевому растяжению R_bt,n принимают равными числовой характеристике класса бетона на осевое растяжение.

Расчетные значения прочностных характеристик бетона

5.1.9 Расчетные значения сопротивления бетона осевому сжатию R_b и осевому растяжениюR_bt определяют по формулам:

; (5.1)

. (5.2)

Значения коэффициента надежности по бетону при сжатии g_b принимают равными:

1,3 — для предельных состояний по несущей способности (первая группа);

1,0 — для предельных состояний по эксплуатационной пригодности (вторая группа).

Значения коэффициента надежности по бетону при растяжении g_bt принимают равными:

1,5 — для предельных состояний по несущей способности при назначении класса бетона по прочности на сжатие;

1,3 — для предельных состояний по несущей способности при назначении класса бетона по прочности на осевое растяжение;

1,0 —- для предельных состояний по эксплуатационной пригодности.

Расчетные значения сопротивления бетона R_b, R_bt, R_b,ser, R_bt,ser (с округлением) в зависимости от класса бетона по прочности на сжатие и осевое растяжение приведены: для предельных состояний первой группы — соответственно в таблицах 5.2 и 5.3, второй группы — в таблице 5.1.

Таблица 5.1

Вид сопротивления	Нормативные значения сопротивления бетона Rb,n и Rbt,n и расчетные значения сопротивления бетона для предельных состояний второй группы Rb,ser и Rbt,ser, МПа, при классе бетона по прочности на сжатие
	В10	В15	В20	В25	В30	В35	В40	В45	В50	В55	В60
Сжатие осевое (призменная прочность)Rb,n, Rb,ser	7,5	11,0	15,0	18,5	22,0	25,5	29,0	32,0	36,0	39,5	43,0
Растяжение осевое Rbt,n,Rbt,ser	0,85	1,1	1,35	1,55	1,75	1,95	2,1	2,25	2,45	2,6	2,75

Таблица 5.2

Вид сопротивления	Расчетные значения сопротивления бетона для предельных состояний первой группы Rb и Rbt, МПа, при классе бетона по прочности на сжатие
	В10	B15	В20	В25	В30	В35	В40	В45	В50	В55	В60
Сжатие осевое (призменная прочность)Rb	6,0	8,5	11,5	14,5	17,0	19,5	22,0	25,0	27,5	30,0	33,0
Растяжение осевое Rbt	0,56	0,75	0,9	1,05	1,15	1,3	1,4	1,5	1,6	1,7	1,8

Таблица 5.3

Вид сопротивления	Расчетные значения сопротивления бетона для предельных состояний первой группы Rbt, МПа, при классе бетона по прочности на осевое растяжение
	Вt 0,8	Вt 1,2	Вt 1,6	Вt 2,0	Вt 2,4	Вt 2,8	Вt 3,2
Растяжение осевое Rbt	0,62	0,93	1,25	1,55	1,85	2,15	2,45

5.1.10 В необходимых случаях расчетные значения прочностных характеристик бетона умножают на следующие коэффициенты условий работы g_bi, учитывающие особенности работы бетона в конструкции (характер нагрузки, условия окружающей среды и т.д.):

а) g_b1 — для бетонных и железобетонных конструкций, вводимый к расчетным значениям сопротивлений R_b и R_bt и учитывающий влияние длительности действия статической нагрузки:

g_b1 = 1,0 — при непродолжительном (кратковременном) действии нагрузки;

g_b1 = 0,9 — при продолжительном (длительном) действии нагрузки;

б) g_b2 — для бетонных конструкций, вводимый к расчетным значениям сопротивления R_b и учитывающий характер разрушения таких конструкций;

g_b2 = 0,9;

в) g_b3 — для бетонных и железобетонных конструкций, бетонируемых в вертикальном положении, вводимый к расчетному значению сопротивления бетона R_b

g_b3 = 0,9.

Влияние попеременного замораживания и оттаивания, а также отрицательных температур учитывают коэффициентом условий работы бетона g_b4 £ 1,0. Для надземных конструкций, подвергаемых атмосферным воздействиям окружающей среды при расчетной температуре наружного воздуха в холодный период минус 40 °С и выше, принимают коэффициент g_b4 = 1,0.

В остальных случаях значения коэффициента g_b4 принимают в зависимости от назначения конструкции и условий окружающей среды согласно специальным указаниям.

Деформационные характеристики бетона

5.1.11 Основными деформационными характеристиками бетона являются значения:

— предельных относительных деформаций бетона при осевом сжатии и растяжении (при однородном напряженном состоянии бетона) e_b0 и e_bt0;

— начального модуля упругости Е_b;

— коэффициента (характеристики) ползучести j_b,cr;

— коэффициента поперечной деформации бетона (коэффициента Пуассона) v_b,P;

— коэффициента линейной температурной деформации бетона a_bt.

5.1.12 Значения предельных относительных деформаций бетона принимают равными:

при непродолжительном действии нагрузки:

e_b0 — 0,002 — при осевом сжатии;

e_bt0 = 0,0001 — при осевом растяжении;

при продолжительном действии нагрузки — по таблице 5.6 в зависимости от относительной влажности окружающей среды.

5.1.13 Значения начального модуля упругости бетона при сжатии и растяжении принимают в зависимости от класса бетона по прочности на сжатие В согласно таблице 5.4.

При продолжительном действии нагрузки значения начального модуля деформаций бетона определяют по формуле

, (5.3)

где j_b,cr — коэффициент ползучести, принимаемый согласно 5.1.14.

5.1.14 Значения коэффициента ползучести бетона j_b,cr принимают в зависимости от условий окружающей среды (относительной влажности воздуха) и класса бетона. Значения коэффициента ползучести бетона приведены в таблице 5.5.

5.1.15 Значение коэффициента поперечной деформации бетона допускается приниматьv_b,P=0,2.

5.1.16 Значение коэффициента линейной температурной деформации бетона при изменении температуры от минус 40 до плюс 50 °С принимают: a_bt = 1 · 10^-5 °С^-1.

Таблица 5.4

Значения начального модуля упругости бетона при сжатии и растяжении Eb, МПа · 10-3, при классе бетона по прочности на сжатие
В10	В15	В20	В25	В30	В35	В40	В45	В50	В55	В60
19,0	24,0	27,5	30,0	32,5	34,5	36,0	37,0	38,0	39,0	39,5

Таблица 5.5

Относительная влажность воздуха окружающей среды, %	Значения коэффициента ползучести jb,cr при классе бетона на сжатие
	В10	В15	В20	В25	В30	В35	В40	В45	В50	В55	В60
Выше 75	2,8	2,4	2,0	1,8	1,6	1,5	1,4	1,3	1,2	1,1	1,0
40-75	3,9	3,4	2,8	2,5	2,3	2,1	1,9	1,8	1,6	1,5	1,4
Ниже 40	5,6	4,8	4,0	3,6	3,2	3,0	2,8	2,6	2,4	2,2	2,0
Примечание — Относительную влажность воздуха окружающей среды принимают по СНиП 23-01 как среднюю месячную относительную влажность наиболее теплого месяца для района строительства.

Таблица 5.6

Относительная влажность воздуха окружающей среды, %	Относительные деформации бетона при продолжительном действии нагрузки
	При сжатии			При растяжении
	eb0·103	eb2·103	eb1,red·103	eb0·103	ebt2·103	ebt1,red·103
Выше 75	3,0	4,2	2,4	0,21	0,27	0,19
40-75	3,4	4,8	2,8	0,24	0,31	0,22
Ниже 40	4,0	5,6	3,4	0,28	0,36	0,26
Примечание — Относительную влажность воздуха окружающей среды принимают по СНиП 23-01 как среднюю месячную относительную влажность наиболее теплого месяца для района строительства.

Диаграммы состояния бетона

5.1.17 В качестве расчетных диаграмм состояния бетона, определяющих связь между напряжениями и относительными деформациями, принимают трехлинейную и двухлинейную диаграммы (рисунок 5.1, а, б).

Диаграммы состояния бетона используют при расчете железобетонных элементов по нелинейной деформационной модели.

5.1.18 При трехлинейной диаграмме (рисунок 5.1, а) сжимающие напряжения бетона s_b в зависимости от относительных деформаций укорочения бетона e_b определяют по формулам:

при 0 £ e_b £ e_b1

; (5.4)

при e_b1 < e_b < e_b0

; (5.5)

при e_b0 £ e_b £ e_b2

s_b = R_b. (5.6)

а — трехлинейная диаграмма состояния сжатого бетона;

б — двухлинейная диаграмма состояния сжатого бетона

Рисунок 5.1 — Диаграммы состояния сжатого бетона

Значения напряжений s_b1 принимают:

s_b1 = 0,6 R_b,

а значения относительных деформаций e_b1 принимают:

.

Значения относительных деформаций e_b2 принимают:

— при непродолжительном действии нагрузки e_b2 = 0,0035;

— при продолжительном действии нагрузки — по таблице 5.6.

Значения R_b, Е_b и e_b0 принимают согласно 5.1.9, 5.1.10, 5.1.12, 5.1.13.

5.1.19 При двухлинейной диаграмме (рисунок 5.1, б) сжимающие напряжения бетона s_b в зависимости от относительных деформаций e_b определяют по формулам:

при 0 £ e_b £ e_b1, где

; (5.7)

при e_b1 £ e_b £ e_b2

s_b = R_b. (5.8)

Значения приведенного модуля деформации бетона Е_b,red принимают:

. (5.9)

Значения относительных деформаций e_b1,red принимают:

— при непродолжительном действии нагрузки e_b1,red = 0,0015;

— при продолжительном действии нагрузки — по таблице 5.6.

Значения R_b, e_b2 принимают, как в 5.1.18.

5.1.20 Растягивающие напряжения бетона s_bt в зависимости от относительных деформаций e_bt определяют по приведенным в 5.1.18 и 5.1.19 диаграммам. При этом расчетные значения сопротивления бетона сжатию R_b заменяют на расчетные значения сопротивления бетона растяжению R_bt согласно 5.1.9, 5.1.10, значения начального модуля упругости E_btопределяют согласно 5.1.13, значения относительной деформации e_bt0 принимают согласно 5.1.12, значения относительной деформации e_bt2 принимают при непродолжительном действии нагрузки e_bt2 = 0,00015, при продолжительном действии нагрузки — по таблице 5.6. Для двухлинейной диаграммы принимают e_bt1,red = 0,00008 — при непродолжительном действии нагрузки, а при продолжительном — по таблице 5.6; значения E_bt,red определяют по формуле (5.9), подставляя в нее R_bt и e_bt1,red.

5.1.21 При расчете прочности железобетонных элементов по нелинейной деформационной модели для определения напряженно-деформированного состояния сжатой зоны бетона используют диаграммы состояния сжатого бетона, приведенные в 5.1.18 и 5.1.19 с деформационными характеристиками, отвечающими непродолжительному действию нагрузки. При этом в качестве наиболее простой используют двухлинейную диаграмму состояния бетона.

5.1.22 При расчете образования трещин в железобетонных конструкциях по нелинейной деформационной модели для определения напряженно-деформированного состояния сжатого и растянутого бетона используют трехлинейную диаграмму состояния бетона, приведенную в 5.1.18 и 5.1.20 с деформационными характеристиками, отвечающими непродолжительному действию нагрузки. Двухлинейную диаграмму (5.1.19) как наиболее простую используют для определения напряженно-деформированного состояния растянутого бетона при упругой работе сжатого бетона.

5.1.23 При расчете деформаций железобетонных элементов по нелинейной деформационной модели при отсутствии трещин для определения напряженно-деформированного состояния в сжатом и растянутом бетоне используют трехлинейную диаграмму состояния бетона с учетом непродолжительного и продолжительного действия нагрузки. При наличии трещин для определения напряженно-деформированного состояния сжатого бетона помимо указанной выше диаграммы используют как наиболее простую двухлинейную диаграмму состояния бетона с учетом непродолжительного и продолжительного действия нагрузки.

5.1.24 При расчете раскрытия нормальных трещин по нелинейной деформационной модели для определения напряженно-деформированного состояния в сжатом бетоне используют диаграммы состояния, приведенные в 5.1.18 и 5.1.19 с учетом непродолжительного действия нагрузки. При этом в качестве наиболее простой используют двухлинейную диаграмму состояния бетона.

5.1.25 Влияние попеременного замораживания и оттаивания, а также отрицательных температур на деформационные характеристики бетона учитывают коэффициентом условий работы g_bt £ 1,0. Для надземных конструкций, подвергаемых атмосферным воздействиям окружающей среды при расчетной температуре наружного воздуха в холодный период минус 40 °С и выше, принимают коэффициент g_bt = 1,0. В остальных случаях значения коэффициента g_bt принимают в зависимости от назначения конструкций и условий окружающей среды.

5.2 АРМАТУРА

Показатели качества арматуры

5.2.1 Для армирования железобетонных конструкций следует применять отвечающую требованиям соответствующих государственных стандартов или утвержденных в установленном порядке технических условий арматуру следующих видов:

— горячекатаную гладкую и периодического профиля с постоянной и переменной высотой выступов (соответственно кольцевой и серповидный профиль) диаметром 6—40 мм;

— термомеханически упрочненную периодического профиля с постоянной и переменной высотой выступов (соответственно кольцевой и серповидный профиль) диаметром 6—40 мм;

— холоднодеформированную периодического профиля диаметром 3—12 мм.

5.2.2 Основным показателем качества арматуры, устанавливаемым при проектировании, является класс арматуры по прочности на растяжение, обозначаемый:

А — для горячекатаной и термомеханически упрочненной арматуры;

В — для холоднодеформированной арматуры.

Классы арматуры по прочности на растяжение А и В отвечают гарантированному значению предела текучести (с округлением) с обеспеченностью не менее 0,95, определяемому по соответствующим стандартам.

Кроме того, в необходимых случаях к арматуре предъявляют требования по дополнительным показателям качества: свариваемость, пластичность, хладостойкость и др.

5.2.3 Для железобетонных конструкций, проектируемых в соответствии с требованиями настоящего Свода правил, следует предусматривать арматуру:

— гладкую класса А240 (A-I);

— периодического профиля классов А300 (A-II), А400 (А-III, А400С), А500 (А500С), В500 (Вр-I, В500С).

В качестве арматуры железобетонных конструкций, устанавливаемой по расчету, следует преимущественно применять арматуру периодического профиля классов А500 и А400, а также арматуру класса В500 в сварных сетках и каркасах. При обосновании экономической целесообразности допускается применять арматуру более высоких классов.

5.2.4 При выборе вида и марок стали для арматуры, устанавливаемой по расчету, а также прокатных сталей для закладных деталей следует учитывать температурные условия эксплуатации конструкций и характер их нагружения.

В конструкциях, эксплуатируемых при статической нагрузке в отапливаемых зданиях, а также на открытом воздухе и в неотапливаемых зданиях при расчетной температуре минус 40 °С и выше, может быть применена арматура всех вышеуказанных классов, за исключением арматуры класса А300 марки стали Ст5пс (диаметром 18—40 мм) и класса А240 марки стали Ст3кп, которые применяют при расчетной температуре минус 30 °С и выше.

При других условиях эксплуатации класс арматуры и марку стали принимают по специальным указаниям.

При проектировании анкеровки арматуры в бетоне и соединений арматуры внахлестку (без сварки) следует учитывать характер поверхности арматуры.

При проектировании сварных соединений арматуры следует учитывать способ изготовления арматуры.

5.2.5 Для монтажных (подъемных) петель элементов сборных железобетонных и бетонных конструкций следует применять горячекатаную арматурную сталь класса А240 марок Ст3сп и Ст3пс.

В случае если возможен монтаж конструкций при расчетной зимней температуре ниже минус 40 °С, для монтажных петель не допускается применять сталь марки Ст3пс.

Нормативные и расчетные значения характеристик арматуры

Нормативные значения прочностных характеристик арматуры

Основной прочностной характеристикой арматуры является нормативное значение сопротивления растяжению R_s,n, принимаемое в зависимости от класса арматуры по таблице 5.7.

Таблица 5.7

Арматура класса	Номинальный диаметр арматуры, мм	Нормативные значения сопротивления растяжению Rs,nи расчетные значения сопротивления растяжению для предельных состояний второй группы Rs,ser, МПа
А240	6-40	240
А300	6-40	300
А400	6-40	400
А500	10-40	500
В500	3-12	500

Расчетные значения прочностных характеристик арматуры

5.2.6 Расчетные значения сопротивления арматуры растяжению R_s определяют по формуле

, (5.10)

где g_s — коэффициент надежности по арматуре, принимаемый равным:

для предельных состояний первой группы:

1,1 — для арматуры классов А240, А300 и А400;

1,15 — для арматуры класса А500;

1,2 — для арматуры класса В500;

1,0 — для предельных состояний второй группы.

Расчетные значения сопротивления арматуры растяжению R_s приведены (с округлением) для предельных состояний первой группы в таблице 5.8, второй группы — в таблице 5.7. При этом значения R_s,n для предельных состояний первой группы приняты равными наименьшим контролируемым значениям по соответствующим ГОСТ.

Расчетные значения сопротивления арматуры сжатию R_sc принимают равными расчетным значениям сопротивления арматуры растяжению R_s, но не более значений, отвечающих деформациям укорочения бетона, окружающего сжатую арматуру: при кратковременном действии нагрузки — не более 400 МПа, при длительном действии нагрузки — не более 500 МПа. Для арматуры класса В500 граничные значения сопротивления сжатию принимаются с коэффициентом условий работы, равным 0,9 (таблица 5.8).

Таблица 5.8

Арматура классов	Расчетные значения сопротивления арматуры для предельных состояний первой группы, МПа
	растяжению		сжатиюRsc
	продольнойRs	поперечной (хомутов и отогнутых стержней) Rsw
А240	215	170	215
А300	270	215	270
А400	355	285	355
А500	435	300	435(400)
В500	415	300	415(360)
Примечание — Значения Rsc в скобках используют только при расчете на кратковременное действие нагрузки.

5.2.7 В необходимых случаях расчетные значения прочностных характеристик арматуры умножают на коэффициенты условий работы g_si, учитывающие особенности работы арматуры в конструкции.

Расчетные значения сопротивления поперечной арматуры (хомутов и отогнутых стержней)R_sw снижают по сравнению с R_s путем умножения на коэффициент условий работы g_s1 = 0,8, но принимают не более 300 МПа. Расчетные значения R_sw (с округлением) приведены в таблице 5.8.

Деформационные характеристики арматуры

5.2.8 Основными деформационными характеристиками арматуры являются значения:

— относительных деформаций удлинения арматуры e_s0 при достижении напряжениями расчетного сопротивления R_s;

— модуля упругости арматуры E_s.

5.2.9 Значения относительных деформаций арматуры e_s0 определяют как упругие при значении сопротивления арматуры R_s

. (5.11)

5.2.10 Значения модуля упругости арматуры E_s принимают одинаковыми при растяжении и сжатии и равными E_s = 2,0 · 10⁵ МПа.

Диаграммы состояния арматуры

5.2.11 При расчете железобетонных элементов по нелинейной деформационной модели в качестве расчетной диаграммы состояния (деформирования) арматуры, устанавливающей связь между напряжениями s_s и относительными деформациями e_s арматуры, принимают двухлинейную диаграмму (рисунок 5.2).

Диаграммы состояния арматуры при растяжении и сжатии принимают одинаковыми.

Рисунок 5.2 — Диаграмма состояния растянутой арматуры

5.2.12 Напряжения в арматуре s_s определяют в зависимости от относительных деформаций e_s согласно диаграмме состояния арматуры по формулам:

при 0 < e_s < e_s0

s_s = e_s E_s; (5.12)

при e_s0 £ e_s £ e_s2

s_s = R_s. (5.13)

Значения e_s0E_s и R_s принимают согласно 5.2.9, 5.2.10 и 5.2.6. Значения относительной деформации e_s2 принимают равными 0,025.

6 РАСЧЕТ ЭЛЕМЕНТОВ БЕТОННЫХ И ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ПЕРВОЙ ГРУППЫ

6.1 РАСЧЕТ БЕТОННЫХ ЭЛЕМЕНТОВ ПО ПРОЧНОСТИ

Общие положения

6.1.1 Бетонные элементы рассчитывают по прочности на действие продольных сжимающих сил, изгибающих моментов и поперечных сил, а также на местное сжатие.

6.1.2 Расчет по прочности бетонных элементов при действии продольной сжимающей силы (внецентренное сжатие) и изгибающего момента следует производить для сечений, нормальных к их продольной оси.

Расчет бетонных элементов прямоугольного, таврового сечений при действии усилий в плоскости симметрии нормального сечения производят по предельным усилиям согласно 6.1.7—6.1.12. В остальных случаях расчет производят на основе нелинейной деформационной модели согласно 6.2.21—6.2.31, принимая в расчетных зависимостях площадь арматуры равной нулю.

6.1.3 Бетонные элементы в зависимости от условий их работы и требований, предъявляемых к ним, рассчитывают по предельным усилиям без учета или с учетом сопротивления бетона растянутой зоны.

Без учета сопротивления бетона растянутой зоны (рисунок 6.1) производят расчет внецентренно сжатых элементов, указанных в 4.1.2, а, принимая, что достижение предельного состояния характеризуется разрушением сжатого бетона. Сопротивление бетона сжатию при расчете по предельным усилиям условно представляют напряжениями, равными R_b, равномерно распределенными по части сжатой зоны (условной сжатой зоны) с центром тяжести, совпадающим с точкой приложения продольной силы (6.1.9).

С учетом сопротивления бетона растянутой зоны (рисунок 6.2) производят расчет элементов, указанных в 4.1.2, б, а также элементов, в которых не допускаются трещины по условиям эксплуатации конструкций. При этом при расчете по предельным усилиям принимают, что предельное состояние характеризуется достижением предельных усилий в бетоне растянутой зоны, определяемых в предположении упругой работы бетона (6.1.9, 6.1.10, 6.1.12).

Рисунок 6.1 — Схема усилий и эпюра напряжений в сечении, нормальном к продольной оси внецентренно сжатого бетонного элемента, рассчитываемого по прочности без учета сопротивления бетона растянутой зоны

Рисунок 6.2 — Схема усилий и эпюра напряжений в сечении, нормальном к продольной оси изгибаемого (внецентренно сжатого) бетонного элемента, рассчитываемого по прочности с учетом сопротивления бетона растянутой зоны

6.1.4 Расчет по прочности бетонных элементов при действии поперечных сил производят из условия, по которому сумма соотношений главного растягивающего напряжения к расчетному сопротивлению бетона осевому растяжению и главного сжимающего напряжения к расчетному сопротивлению бетона осевому сжатию не должна превышать 1,0.

6.1.5 Расчет по прочности бетонных элементов на действие местной нагрузки (местное сжатие) производят согласно указаниям 6.2.42—6.2.44.

6.1.6 В бетонных элементах в случаях, указанных в 8.3.5, необходимо предусматривать конструктивную арматуру.

Расчет внецентренно сжатых элементов по предельным усилиям

6.1.7 При расчете внецентренно сжатых бетонных элементов следует учитывать случайный начальный эксцентриситет e₀ продольной силы, определяемый согласно указаниям 4.2.6.

6.1.8 При гибкости элементов необходимо учитывать влияние на их несущую способность прогибов путем умножения значений е₀ на коэффициент h, определяемый согласно 6.1.11.

6.1.9 Расчет внецентренно сжатых бетонных элементов при расположении продольной сжимающей силы в пределах поперечного сечения элемента производят из условия

N £ R_b A_b, (6.1)

где A_b — площадь сжатой зоны бетона, определяемая из условия, что ее центр тяжести совпадает с точкой приложения продольной силы N (с учетом прогиба).

Для элементов прямоугольного сечения

. (6.2)

Допускается расчет внецентренно сжатых элементов прямоугольного сечения при эксцентриситете продольной силы е₀ £ h/30 и l₀ £ 20h производить из условия

N £ j R_b A, (6.3)

где А — площадь поперечного сечения элемента;

j — коэффициент, принимаемый при длительном действии нагрузки по таблице 6.1 в зависимости от гибкости элемента, при кратковременном действии нагрузки значения j определяют по линейному закону, принимая

j = 0,9 при = 10 и j = 0,85 при = 20;

l₀ — расчетная длина элемента, определяемая как для железобетонных элементов.

Таблица 6.1

l0/h	6	10	15	20
j	0,92	0,9	0,8	0,6

Внецентренно сжатые бетонные элементы, в которых появление трещин не допускается по условиям эксплуатации, независимо от расчета из условия (6.1) должны быть проверены с учетом сопротивления бетона растянутой зоны из условия

. (6.4)

Для элементов прямоугольного сечения условие (6.4) имеет вид

. (6.5)

В формулах (6.4) и (6.5):

y_t — расстояние от центра тяжести сечения элемента до наиболее растянутого волокна;

h — коэффициент, определяемый согласно указаниям 6.1.11.

6.1.10 Расчет внецентренно сжатых элементов при расположении продольной сжимающей силы за пределами поперечного сечения элемента производят из условий (6.4) и (6.5).

6.1.11 Значение коэффициента h, учитывающего влияние прогиба на значение эксцентриситета продольной силы е₀, определяют по формуле

, (6.6)

где N_cr — условная критическая сила, определяемая по формуле

, (6.7)

где D — жесткость элемента, определяемая как для железобетонных элементов, но без учета арматуры согласно 6.2.16.

Расчет изгибаемых элементов по предельным усилиям

6.1.12 Расчет изгибаемых бетонных элементов следует производить из условия

М £ М_ult, (6.8)

где М_ult — предельный изгибающий момент, который может быть воспринят сечением элемента.

Значение М_ult определяют по формуле

М_ult = R_bt W, (6.9)

где W — момент сопротивления сечения для крайнего растянутого волокна.

Для элементов прямоугольного сечения

. (6.10)

6.2 РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО ПРОЧНОСТИ

Общие положения

6.2.1 Железобетонные элементы рассчитывают по прочности на действие изгибающих моментов, продольных сил, поперечных сил, крутящих моментов и на местное действие нагрузки (местное сжатие, продавливание).

Расчет по прочности железобетонных элементов на действие изгибающих моментов и продольных сил

Общие положения

6.2.2 Расчет по прочности железобетонных элементов при действии изгибающих моментов и продольных сил (внецентренное сжатие или растяжение) следует производить для сечений, нормальных к их продольной оси.

Расчет по прочности нормальных сечений железобетонных элементов следует производить на основе нелинейной деформационной модели согласно 6.2.21—6.2.31.

Допускается расчет железобетонных элементов прямоугольного, таврового и двутаврового сечений с арматурой, расположенной у перпендикулярных плоскости изгиба граней элемента, при действии усилий в плоскости симметрии нормальных сечений производить на основе предельных усилий согласно 6.2.5—6.2.17.

6.2.3 При расчете внецентренно сжатых элементов следует учитывать влияние прогиба на их несущую способность, как правило, путем расчета конструкций по деформированной схеме.

Допускается производить расчет конструкций по недеформированной схеме, учитывая при гибкости влияние прогиба элемента на его прочность, путем умножения начального эксцентриситета е₀ на коэффициент h, определяемый согласно указаниям 6.2.16.

6.2.4 Для железобетонных элементов, у которых предельное усилие по прочности оказывается меньше предельного усилия по образованию трещин (7.2.5—7.2.11), площадь сечения продольной растянутой арматуры должна быть увеличена по сравнению с требуемой из расчета по прочности не менее чем на 15 % или соответствовать предельному усилию по образованию трещин.

Расчет по прочности нормальных сечений по предельным усилиям

6.2.5 Предельные усилия в сечении, нормальном к продольной оси элемента, следует определять исходя из следующих предпосылок:

— сопротивление бетона растяжению принимают равным нулю;

— сопротивление бетона сжатию представляется напряжениями, равными R_b и равномерно распределенными по сжатой зоне бетона;

— деформации (напряжения) в арматуре определяют в зависимости от высоты сжатой зоны бетона;

— растягивающие напряжения в арматуре принимают не более расчетного сопротивления растяжению R_s;

— сжимающие напряжения в арматуре принимают не более расчетного сопротивления сжатию R_sc.

6.2.6 Расчет по прочности нормальных сечений следует производить в зависимости от соотношения между значением относительной высоты сжатой зоны бетона , определяемым из соответствующих условий равновесия, и значением граничной относительной высоты сжатой зоны x_R, при котором предельное состояние элемента наступает одновременно с достижением в растянутой арматуре напряжения, равного расчетному сопротивлению R_s.

6.2.7 Значение x_R определяют по формуле

, (6.11)

где e_s,el — относительная деформация растянутой арматуры при напряжениях, равных R_s

; (6.12)

e_b,ult — относительная деформация сжатого бетона при напряжениях, равных R_b, принимаемая равной 0,0035.

6.2.8 При расчете внецентренно сжатых железобетонных элементов в начальном эксцентриситете приложения продольной силы е₀ следует учитывать случайный эксцентриситет е₀, принимаемый по указаниям 4.2.6.

Расчет изгибаемых элементов

6.2.9 Расчет по прочности сечений изгибаемых элементов производят из условия

М £ М_ult, (6.13)

где М_ult — предельный изгибающий момент, который может быть воспринят сечением элемента.

6.2.10 Значение М_ult для изгибаемых элементов прямоугольного сечения (рисунок 6.3) при определяют по формуле

, (6.14)

при этом высоту сжатой зоны х определяют по формуле

. (6.15)

6.2.11 Значение М_ult для изгибаемых элементов, имеющих полку в сжатой зоне (тавровые и двутавровые сечения), при определяют в зависимости от положения границы сжатой зоны:

а) если граница проходит в полке (рисунок 6.4), т.е. соблюдается условие

, (6.16)

значение М_ult определяют по 6.2.10 как для прямоугольного сечения шириной b‘_f;

Рисунок 6.3 — Схема усилий и эпюра напряжений в сечении, нормальном к продольной оси изгибаемого железобетонного элемента, при его расчете по прочности

а — в полке; б — в ребре

Рисунок 6.4 — Положение границы сжатой зоны в сечении изгибаемого железобетонного элемента

б) если граница проходит в ребре (рисунок 6.4, б), т.е. условие (6.16) не соблюдается, значение М_ult определяют по формуле

, (6.17)

при этом высоту сжатой зоны бетона х определяют по формуле

, (6.18)

6.2.12 Значение b‘_f, вводимое в расчет, принимают из условия, что ширина свеса полки в каждую сторону от ребра должна быть не более ¹/₆ пролета элемента и не более:

а) при наличии поперечных ребер или при h‘_f > 0,1 h — ^l/₂ расстояния в свету между продольными ребрами;

б) при отсутствии поперечных ребер (или при расстояниях между ними больших, чем расстояния между продольными ребрами) и h‘_f < 0,1 h – 6 h‘_f;

в) при консольных свесах полки:

при h‘_f ³ 0,1 h – 6 h‘_f;

при 0,05 h £ h‘_f < 0,1 h – 3 h‘_f;

при h‘_f < 0,05 h — свесы не учитывают.

6.2.13 При расчете по прочности изгибаемых элементов рекомендуется соблюдать условие x£ x_R h₀.

В случае когда по конструктивным соображениям или из расчета по предельным состояниям второй группы площадь растянутой арматуры принята большей, чем это требуется для соблюдения условия x £ x_R h₀, допускается предельный изгибающий момент M_ultопределять по формулам (6.14) или (6.17), подставляя в них значения высоты сжатой зоны x= x_R h₀.

6.2.14 При симметричном армировании, когда R_s A = R_sc A‘_s, значение M_ult определяют по формуле

M_ult = R_s A_s (h₀ – a’). (6.19)

Если вычисленная без учета сжатой арматуры (А’_s = 0) высота сжатой зоны х < 2а, в формулу (6.19) подставляют вместо а значение .

Расчет внецентренно сжатых элементов

6.2.15 Расчет по прочности прямоугольных сечений внецентренно сжатых элементов производят из условия

Ne £ R_b bx (h₀ — 0,5х) + R_sc A’_s (h₀ — a’), (6.20)

где е — расстояние от точки приложения силы N до центра тяжести сечения растянутой или наименее сжатой (при полностью сжатом сечении элемента) арматуры, равное:

.

Здесь h — коэффициент, учитывающий влияние продольного изгиба (прогиба) элемента на его несущую способность и определяемый согласно 6.2.16.

Высоту сжатой зоны х определяют:

а) при (рисунок 6.5) по формуле

; (6.21)

б) при по формуле

. (6.22)

6.2.16 Значение коэффициента h при расчете конструкций по недеформированной схеме определяют по формуле

, (6.23)

где N_cr — условная критическая сила, определяемая по формуле

, (6.24)

где D — жесткость железобетонного элемента;

l₀ — расчетная длина элемента, определяемая согласно 6.2.18.

Допускается значение D определять по формуле

D = k_b E_b I + k_s E_s I_s, (6.25)

где E_b, E_s — модули упругости соответственно бетона и арматуры;

I, I_s — моменты инерции площадей сечения соответственно бетона и всей продольной арматуры относительно центра тяжести поперечного сечения элемента;

;

k_s = 0,7;

j_l — коэффициент, учитывающий влияние длительности действия нагрузки

;

M₁M_l1 — моменты относительно центра наиболее растянутого или наименее сжатого (при целиком сжатом сечении) стержня арматуры соответственно от действия полной нагрузки и от действия постоянных и длительных нагрузок;

d_е — относительное значение эксцентриситета продольной силы , где , принимаемое не менее 0,15.

Рисунок 6.5 — Схема усилий и эпюра напряжений в сечении, нормальном к продольной оси внецентренно сжатого железобетонного элемента, при расчете его по прочности

Допускается уменьшать значение коэффициента h с учетом распределения изгибающих моментов по длине элемента, характера его деформирования и влияния прогибов на значение изгибающего момента в расчетном сечении путем расчета конструкции как упругой системы.

6.2.17 Расчет по прочности прямоугольных сечений внецентренно сжатых элементов с арматурой, расположенной у противоположных в плоскости изгиба сторон сечения, при эксцентриситете продольной силы и гибкости допускается производить из условия

N £ N_ult, (6.26)

где N_ult — предельное значение продольной силы, которую может воспринять элемент, определяемое по формуле

N_ult = j (R_b A + R_sc A_s,tot). (6.27)

Здесь A_s,tot — площадь всей продольной арматуры в сечении элемента;

j — коэффициент, принимаемый при длительном действии нагрузки по таблице 6.2 в зависимости от гибкости элемента; при кратковременном действии нагрузки значения j определяют по линейному закону, принимая j = 0,9 при и j = 0,85 при .

Таблица 6.2

l0 / h	6	10	15	20
j	0,92	0,9	0,83	0,7

6.2.18 Расчетную длину l₀ внецентренно сжатого элемента определяют как для элементов рамной конструкции с учетом ее деформированного состояния при наиболее невыгодном для данного элемента расположении нагрузки, принимая во внимание неупругие деформации материалов и наличие трещин.

Допускается расчетную длину l₀ элементов постоянного поперечного сечения по длине l при действии продольной силы принимать равной:

а) для элементов с шарнирным опиранием на двух концах — 1,0l;

б) для элементов с жесткой заделкой (исключающей поворот опорного сечения) на одном конце и незакрепленным другим концом (консоль) — 2,0l;

в) для элементов с шарнирным несмещаемым опиранием на одном конце, а на другом конце:

с жесткой (без поворота) заделкой — 0,7l;

с податливой (допускающей ограниченный поворот) заделкой — 0,9l;

г) для элементов с податливым шарнирным опиранием (допускающим ограниченное смещение опоры) на одном конце, а на другом конце:

с жесткой (без поворота) заделкой — 1,5l;

с податливой (с ограниченным поворотом) заделкой — 2,0l;

д) для элементов с несмещаемыми заделками на двух концах:

жесткими (без поворота) — 0,5l;

податливыми (с ограниченным поворотом) — 0,8l;

е) для элементов с ограниченно смещаемыми заделками на двух концах:

жесткими (без поворота) — 0,8l;

податливыми (с ограниченным поворотом) — 1,2l.

Расчет центрально-растянутых элементов

6.2.19 Расчет по прочности сечений центрально-растянутых элементов следует производить из условия

N £ N_ult, (6.28)

где N_ult — предельное значение продольной растягивающей силы, которое может быть воспринято элементом.

Значение силы N_ult определяют по формуле

N_ult = R_s A_s,tot, (6.29)

где A_s,tot — площадь сечения всей продольной арматуры.

Расчет внецентренно растянутых элементов

6.2.20 Расчет по прочности прямоугольных сечений внецентренно растянутых элементов следует производить в зависимости от положения продольной силы N:

а) если продольная сила N приложена между равнодействующими усилий в арматуре S и S‘(рисунок 6.6, а), — из условий:

Ne £ M_ult; (6.30)

Ne’ < M’_ult, (6.31)

где Ne и Ne‘ — усилия от внешних нагрузок;

M_ult и M‘_ult — предельные усилия, которые может воспринять сечение.

Усилия M_ult и M‘_ult определяют по формулам:

M_ult = R_s A’_s (h₀ – a’); (6.32)

M’_ult = R_s A_s (h₀ – a’); (6.33)

б) если продольная сила N приложена за пределами расстояния между равнодействующими усилий в арматуре S и S‘ (рисунок 6.6, б), из условия (6.30) определяют предельный моментM_ult по формуле

M_ult = R_b bx (h₀ – 0,5x) + R_sc A’_s (h₀ – a’); (6.34)

при этом высоту сжатой зоны х определяют по формуле

. (6.35)

Если полученное из расчета по формуле (6.35) значение х > x_Rh₀ в формулу (6.34) подставляют х = x_Rh₀, где x_R определяют согласно указаниям 6.2.7.

a — между равнодействующими усилий в арматуре S и S’; б — за пределами расстояния между равнодействующими усилий в арматуре S и S’

Рисунок 6.6 — Схема усилий и эпюра напряжений в сечении, нормальном к продольной оси внецентренно растянутого железобетонного элемента, при расчете его по прочности при приложении продольной силы N

Расчет по прочности нормальных сечений на основе нелинейной деформационной модели

6.2.21 При расчете по прочности усилия и деформации в сечении, нормальном к продольной оси элемента, определяют на основе нелинейной деформационной модели, использующей уравнения равновесия внешних сил и внутренних усилий в сечении элемента, а также следующие положения:

— распределение относительных деформаций бетона и арматуры по высоте сечения элемента принимают по линейному закону (гипотеза плоских сечений);

— связь между осевыми напряжениями и относительными деформациями бетона и арматуры принимают в виде диаграмм состояния (деформирования) бетона и арматуры (5.1.17, 5.2.11);

— сопротивление бетона растянутой зоны допускается не учитывать, принимая при e_bi ³ 0 напряжения s_bi = 0. В отдельных случаях (например, изгибаемые и внецентренно сжатые бетонные конструкции, в которых не допускают трещины) расчет по прочности производят с учетом работы растянутого бетона.

6.2.22 Переход от эпюры напряжений в бетоне к обобщенным внутренним усилиям определяют с помощью процедуры численного интегрирования напряжений по нормальному сечению. Для этого нормальное сечение условно разделяют на малые участки: при косом внецентренном сжатии (растяжении) и косом изгибе — по высоте и ширине сечения; при внецентренном сжатии (растяжении) и изгибе в плоскости оси симметрии поперечного сечения элемента — только по высоте сечения. Напряжения в пределах малых участков принимают равномерно распределенными (усредненными).

6.2.23 При расчете элементов с использованием деформационной модели принимают:

— значения сжимающей продольной силы, а также сжимающих напряжений и деформаций укорочения бетона и арматуры — со знаком «минус»;

— значения растягивающей продольной силы, а также растягивающих напряжений и деформаций удлинения бетона и арматуры — со знаком «плюс».

Знаки координат центров тяжести арматурных стержней и выделенных участков бетона, а также точки приложения продольной силы принимают в соответствии с назначенной системой координат XOY. В общем случае начало координат этой системы (точка О на рисунке 6.7) располагают в произвольном месте в пределах поперечного сечения элемента.

Рисунок 6.7 — Расчетная схема нормального сечения железобетонного элемента

6.2.24 При расчете нормальных сечений по прочности (рисунок 6.7) в общем случае используют:

уравнения равновесия внешних сил и внутренних усилий в нормальном сечении элемента:

; (6.36)

; (6.37)

; (6.38)

уравнения, определяющие распределение деформаций по сечению элемента:

; (6.39)

; (6.40)

зависимости, связывающие напряжения и относительные деформации бетона и арматуры:

; (6.41)

; (6.42)

В уравнениях (6.36)—(6.42):

М_х, М_y — изгибающие моменты от внешней нагрузки относительно выбранных и располагаемых в пределах поперечного сечения элемента координатных осей (соответственно действующих в плоскостях XOZ и YOZ или параллельно им), определяемые по формулам:

М_x = M_xd + Ne_x, (6.43)

М_у = M_yd + Ne_y, (6.44)

где M_xd, M_yd — изгибающие моменты в соответствующих плоскостях от внешней нагрузки, определяемые из статического расчета конструкции;

N — продольная сила от внешней нагрузки;

e_х, е_y — расстояния от точки приложения силы N до соответствующих выбранных осей;

А_bi, Z_bm, Z_byi, s_bi — площадь, координаты центра тяжести i-го участка бетона и напряжение на уровне его центра тяжести;

A_sj, Z_sxj, Z_syj, s_sj — площадь, координаты центра тяжести j-го стержня арматуры и напряжение в нем;

e₀ — относительная деформация волокна, расположенного на пересечении выбранных осей (в точке О);

, — кривизна продольной оси в рассматриваемом поперечном сечении элемента в плоскостях действия изгибающих моментов М_х и М_y;

Е_b — начальный модуль упругости бетона;

E_sj — модуль упругости j-го стержня арматуры;

v_bi — коэффициент упругости бетона i-го участка;

v_sj — коэффициент упругости j-го стержня арматуры.

Коэффициенты v_bi и v_sj принимают по соответствующим диаграммам состояния бетона и арматуры, указанным в 5.1.17, 5.2.11.

Значения коэффициентов v_bj и v_sj определяют как соотношение значений напряжений и деформаций для рассматриваемых точек соответствующих диаграмм состояния бетона и арматуры, принятых в расчете, деленное на модуль упругости бетона Е_b и арматуры E_s (при двухлинейной диаграмме состояния бетона — на приведенный модуль деформации E_b,red). При этом используют зависимости «напряжение — деформация» (5.4)—(5.8), (5.12) и (5.13) на рассматриваемых участках диаграмм.

; (6.45)

. (6.46)

6.2.25 Расчет нормальных сечений железобетонных элементов по прочности производят из условий

; (6.47)

, (6.48)

где e_b,max — относительная деформация наиболее сжатого волокна бетона в нормальном сечении элемента от действия внешней нагрузки;

e_s,max — относительная деформация наиболее растянутого стержня арматуры в нормальном сечении элемента от действия внешней нагрузки;

e_b,ult — предельное значение относительной деформации бетона при сжатии, принимаемое согласно указаниям 6.2.31;

e_s,ult — предельное значение относительной деформации удлинения арматуры, принимаемое согласно указаниям 6.2.31.

6.2.26 Для железобетонных элементов, на которые действуют изгибающие моменты двух направлений и продольная сила (рисунок 6.7), деформации бетона e_b,max и арматуры e_s,max в нормальном сечении произвольной формы определяют из решения системы уравнений (6.49)—(6.51) с использованием уравнений (6.39) и (6.40):

; (6.49)

; (6.50)

; (6.51)

Жесткостные характеристики D_ij (i, j = 1, 2, 3) в уравнениях (6.49)—(6.51) определяют по формулам:

; (6.52)

; (6.53)

; (6.54)

; (6.55)

; (6.56)

; (6.57)

Обозначения в формулах см. 6.2.24.

6.2.27 Для железобетонных элементов, на которые действуют только изгибающие моменты двух направлений М_х и М_у (косой изгиб), в уравнении (6.51) принимают N = 0.

6.2.28 Для внецентренно сжатых в плоскости симметрии поперечного сечения железобетонных элементов и расположения оси Х в этой плоскости М_y = 0 и D₁₂ = D₂₂ = D₂₃ = 0. В этом случае уравнения равновесия имеют вид:

; (6.58)

. (6.59)

6.2.29 Для изгибаемых в плоскости симметрии поперечного сечения железобетонных элементов и расположения оси X в этой плоскости N = 0, M_y = 0, D₁₂ = D₂₂ = D₂₃ = 0. В этом случае уравнения равновесия имеют вид:

; (6.60)

. (6.61)

6.2.30 Расчет по прочности нормальных сечений внецентренно сжатых бетонных элементов, указанных в 4.1.2а, производят из условия (6.47) согласно указаниям 6.2.25—6.2.29, принимая в формулах 6.2.26 для определения D_ij площадь арматуры A_sj = 0.

Для изгибаемых и внецентренно сжатых бетонных элементов, в которых не допускаются трещины, расчет производят с учетом работы растянутого бетона в поперечном сечении элемента из условия

, (6.62)

где e_bt,max — относительная деформация наиболее растянутого волокна бетона в нормальном сечении элемента от действия внешней нагрузки, определяемая согласно 6.2.26—6.2.29;

e_bt,ult — предельное значение относительной деформации бетона при растяжении, принимаемое согласно указаниям 6.2.31.

6.2.31 Предельные значения относительных деформаций бетона e_b,ult (e_bt,ult) принимают при двузначной эпюре деформаций (сжатие и растяжение) в поперечном сечении бетона элемента (изгиб, внецентренное сжатие или растяжение с большими эксцентриситетами) равными e_b2 (e_bt2).

При внецентренном сжатии или растяжении элементов и распределении в поперечном сечении бетона элемента деформаций только одного знака предельные значения относительных деформаций бетона e_b,ult (e_bt,ult) определяют в зависимости от соотношения деформаций бетона на противоположных гранях сечения элемента e₁ и e₂ (|e₂| ³ |e₁|) по формулам:

; (6.63)

; (6.64)

где e_b0, e_bt0, e_b2, e_bt2 — деформационные параметры расчетных диаграмм состояния бетона (5.1.12, 5.1.18, 5.1.20).

Предельное значение относительной деформации арматуры e_s,ult принимают равным 0,025.

Расчет по прочности железобетонных элементов при действии поперечных сил

Общие положения

6.2.32 Расчет по прочности железобетонных элементов при действии поперечных сил производят на основе модели наклонных сечений.

При расчете по модели наклонных сечений должны быть обеспечены прочность элемента по полосе между наклонными сечениями и по наклонному сечению на действие поперечных сил, а также прочность по наклонному сечению на действие момента.

Прочность по наклонной полосе характеризуется максимальным значением поперечной силы, которое может быть воспринято наклонной полосой, находящейся под воздействием сжимающих усилий вдоль полосы и растягивающих усилий от поперечной арматуры, пересекающей наклонную полосу. При этом прочность бетона определяют по сопротивлению бетона осевому сжатию с учетом влияния сложного напряженного состояния в наклонной полосе.

Расчет по наклонному сечению на действие поперечных сил производят на основе уравнения равновесия внешних и внутренних поперечных сил, действующих в наклонном сечении с длиной проекции с на продольную ось элемента. Внутренние поперечные силы включают поперечную силу, воспринимаемую бетоном в наклонном сечении, и поперечную силу, воспринимаемую пересекающей наклонное сечение поперечной арматурой. При этом поперечные силы, воспринимаемые бетоном и поперечной арматурой, определяют по сопротивлениям бетона и поперечной арматуры растяжению с учетом длины проекции снаклонного сечения.

Расчет по наклонному сечению на действие момента производят на основе уравнения равновесия моментов от внешних и внутренних сил, действующих в наклонном сечении с длиной проекции с на продольную ось элемента. Моменты от внутренних сил включают момент, воспринимаемый пересекающей наклонное сечение продольной растянутой арматурой, и момент, воспринимаемый пересекающей наклонное сечение поперечной арматурой. При этом моменты, воспринимаемые продольной и поперечной арматурой, определяют по сопротивлениям продольной и поперечной арматуры растяжению с учетом длины проекции с наклонного сечения.

Расчет железобетонных элементов по полосе между наклонными сечениями

6.2.33 Расчет изгибаемых железобетонных элементов по бетонной полосе между наклонными сечениями производят из условия

Q £ j_b1R_b b h₀, (6.65)

где Q — поперечная сила в нормальном сечении элемента;

j_b1 — коэффициент, принимаемый равным 0,3.

Расчет железобетонных элементов по наклонным сечениям на действие поперечных сил

6.2.34 Расчет изгибаемых элементов по наклонному сечению (рисунок 6.8) производят из условия

Q £ Q_b + Q_sw, (6.66)

где Q — поперечная сила в наклонном сечении с длиной проекции с на продольную ось элемента, определяемая от всех внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения; при этом учитывают наиболее опасное загружение в пределах наклонного сечения;

Q_b — поперечная сила, воспринимаемая бетоном в наклонном сечении;

Q_sw — поперечная сила, воспринимаемая поперечной арматурой в наклонном сечении.

Поперечную силу Q_b определяют по формуле

, (6.67)

но принимают не более 2,5 R_bt b h₀ и не менее 0,5 R_bt b h₀;

j_b2 — коэффициент, принимаемый равным 1,5.

Усилие Q_sw для поперечной арматуры, нормальной к продольной оси элемента, определяют по формуле

Q_sw = j_sw q_sw c, (6.68)

где j_sw — коэффициент, принимаемый равным 0,75;

q_sw— усилие в поперечной арматуре на единицу длины элемента

. (6.69)

Рисунок 6.8 — Схема усилий при расчете железобетонных элементов по наклонному сечению на действие поперечных сил

Расчет производят для ряда расположенных по длине элемента наклонных сечений при наиболее опасной длине проекции наклонного сечения с. При этом длину с в формуле (6.68) принимают не более 2,0 h₀.

Допускается производить расчет наклонных сечений, не рассматривая наклонные сечения при определении поперечной силы от внешней нагрузки, из условия

Q₁ £ Q_b1 + Q_sw,1, (6.70)

где Q₁ — поперечная сила в нормальном сечении от внешней нагрузки;

Q_b1 = 0,5 R_bt b h₀; (6.71)

Q_sw,1 = q_sw h₀. (6.72)

При расположении нормального сечения, в котором учитывают поперечную силу Q₁, вблизи опоры на расстоянии а менее 2,5h₀ расчет из условия (6.70) производят, умножая значенияQ_b1, определяемые по формуле (6.71), на коэффициент, равный , но принимают значениеQ_b1 не более 2,5 R_bt b h₀.

При расположении нормального сечения, в котором учитывают поперечную силу Q₁ на расстоянии а менее h₀ расчет из условия (6.70) производят, умножая значение Q_sw,1определяемое по формуле (6.72), на коэффициент, равный a/h₀.

Поперечную арматуру учитывают в расчете, если соблюдается условие

q_sw ³ 0,25 R_bt b.

Можно учитывать поперечную арматуру и при невыполнении этого условия, если в условии (6.66) принимать

.

Шаг поперечной арматуры, учитываемой в расчете, должен быть не больше значения .

При отсутствии поперечной арматуры или нарушении указанных выше требований расчет производят из условий (6.66) или (6.70), принимая усилия Q_sw или Q_sw,1 равными нулю.

Поперечная арматура должна отвечать конструктивным требованиям, приведенным в 8.3.9-8.3.17.

Расчет железобетонных элементов по наклонным сечениям на действие моментов

6.2.35 Расчет железобетонных элементов по наклонным сечениям на действие моментов (рисунок 6.9) производят из условия

M £ M_s + M_sw, (6.73)

где М — момент в наклонном сечении с длиной проекции с на продольную ось элемента, определяемый от всех внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения, относительно конца наклонного сечения (точка О), противоположного концу, у которого располагается проверяемая продольная арматура, испытывающая растяжение от момента в наклонном сечении; при этом учитывают наиболее опасное загружение в пределах наклонного сечения;

M_s — момент, воспринимаемый продольной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения (точка О);

M_sw — момент, воспринимаемый поперечной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения (точка О).

Рисунок 6.9 — Схема усилий при расчете железобетонных элементов по наклонному сечению на действие моментов

Момент M_s определяют по формуле

M_s = N_s z_s, (6.74)

где N_s — усилие в продольной растянутой арматуре, принимаемое равным: R_sA_s, а в зоне анкеровки — определяемое согласно 8.3.18-8.3.25;

z_s — плечо внутренней пары сил; допускается принимать z_s = 0,9 h₀.

Момент M_sw для поперечной арматуры, нормальной к продольной оси элемента, определяют по формуле

M_sw = 0,5 Q_sw c, (6.75)

где Q_sw — усилие в поперечной арматуре, принимаемое равным q_sw с;

q_sw — определяют по формуле (6.69), а с принимают в пределах от 1,0 h₀ до 2,0 h₀.

Расчет производят для наклонных сечений, расположенных по длине элемента на его концевых участках и в местах обрыва продольной арматуры, при наиболее опасной длине проекции наклонного сечения с, принимаемой в указанных выше пределах.

Допускается производить расчет наклонных сечений, принимая в условии (6.73) момент М в наклонном сечении при длине проекции с на продольную ось элемента равным 2,0h₀, а момент M_sw — равным .

При отсутствии поперечной арматуры расчет наклонных сечений производят из условия (6.73), принимая момент М в наклонном сечении при длине проекции с на продольную ось элемента равным 2,0 h₀, а момент М_sw — равным нулю.

Расчет по прочности железобетонных элементов при действии крутящих моментов

Общие положения

6.2.36 Расчет по прочности железобетонных элементов на действие крутящих моментов производят на основе модели пространственных сечений.

При расчете по модели пространственных сечений рассматривают сечения, образованные наклонными отрезками прямых, следующими по трем растянутым граням элемента, и замыкающим отрезком прямой по четвертой сжатой грани элемента.

Расчет железобетонных элементов на действие крутящих моментов производят по прочности элемента между пространственными сечениями и по прочности пространственных сечений.

Прочность по бетону между пространственными сечениями характеризуется максимальным значением крутящего момента, определяемым по сопротивлению бетона осевому сжатию с учетом напряженного состояния в бетоне между пространственными сечениями.

Расчет по пространственным сечениям производят на основе уравнений равновесия всех внутренних и внешних сил относительно оси, расположенной в центре сжатой зоны пространственного сечения элемента. Внутренние моменты включают момент, воспринимаемый арматурой, следующей вдоль оси элемента, и арматурой, следующей поперек оси элемента, пересекающей пространственное сечение и расположенной в растянутой зоне пространственного сечения и у растянутой грани элемента, противоположной сжатой зоне пространственного сечения. При этом усилия, воспринимаемые арматурой, определяют соответственно по расчетным значениям сопротивления растяжению продольной и поперечной арматуры.

При расчете рассматривают все положения пространственного сечения, принимая сжатую зону пространственного сечения у нижней, боковой и верхней граней элемента.

Расчет на совместное действие крутящих и изгибающих моментов, а также крутящих моментов и поперечных сил производят исходя из уравнений взаимодействия между соответствующими силовыми факторами.

Расчет на действие крутящего момента

6.2.37 Расчет по прочности элемента между пространственными сечениями производят из условия

T £ 0,1 R_b b² h, (6.76)

где Т — крутящий момент от внешних нагрузок в нормальном сечении элемента;

b и h — соответственно меньший и больший размеры поперечного сечения элемента.

6.2.38 Расчет по прочности пространственных сечений производят из условия (рисунок 6.10)

T £ T_sw + T_s, (6.77)

где Т — крутящий момент в пространственном сечении, определяемый от всех внешних сил, расположенных по одну сторону пространственного сечения;

T_sw — крутящий момент, воспринимаемый арматурой пространственного сечения, расположенной в поперечном по отношению к оси элемента направлении;

T_s — крутящий момент, воспринимаемый арматурой пространственного сечения, расположенной в продольном направлении.

Значение соотношения между усилиями в поперечной и продольной арматуре, учитываемое в условии (6.77), приведено ниже.

Крутящий момент T_sw определяют по формуле

T_sw = 0,9 N_sw Z₂, (6.78)

а крутящий момент T_s — по формуле

, (6.79)

где N_sw — усилие в арматуре, расположенной в поперечном направлении; для арматуры, нормальной к продольной оси элемента, усилие N_sw определяют по формуле

N_sw = q_sw,1c_sw, (6.80)

а — растянутая арматура у нижней грани элемента; б — растянутая арматура у боковой грани элемента

Рисунок 6.10 — Схемы усилий в пространственных сечениях при расчете на действие крутящего момента

q_sw,1 — усилие в этой арматуре на единицу длины элемента

, (6.81)

A_sw,1 — площадь сечения арматуры, расположенной в поперечном направлении;

s_w — шаг этой арматуры;

c_sw — длина проекции растянутой стороны пространственного сечения на продольную ось элемента

c_sw = d c, (6.82)

d — коэффициент, учитывающий соотношение размеров поперечного сечения

; (6.83)

с — длина проекции сжатой стороны пространственного сечения на продольную ось элемента;

N_s — усилие в продольной арматуре, расположенной у рассматриваемой грани элемента

N_s = R_s A_s,1; (6.84)

A_s,1 — площадь сечения продольной арматуры, расположенной у рассматриваемой грани элемента;

Z₁ и Z₂ — длина стороны поперечного сечения у рассматриваемой растянутой грани элемента и длина другой стороны поперечного сечения элемента.

Соотношение принимают в пределах от 0,5 до 1,5. В том случае, если значение выходит за указанные пределы, в расчете учитывают такое количество арматуры (продольной или поперечной), при котором значение оказывается в указанных пределах.

Расчет производят для ряда пространственных сечений, расположенных по длине элемента, при наиболее опасной длине проекции пространственного сечения с на продольную ось элемента. При этом значение с принимают не более 2Z₂ + Z₁ и не более .

Допускается расчет на действие крутящего момента производить, не рассматривая пространственные сечения при определении крутящего момента от внешней нагрузки, из условия

Т₁ £ Т_sw,1 + T_s,1, (6.85)

где Т₁ — крутящий момент в нормальном сечении элемента;

T_sw,1 — крутящий момент, воспринимаемый арматурой, расположенной у рассматриваемой грани элемента в поперечном направлении, и определяемый по формуле

T_sw,1 = q_sw,1 d Z₁Z₂; (6.86)

T_s,1 — крутящий момент, воспринимаемый продольной арматурой, расположенной у рассматриваемой грани элемента, и определяемый по формуле

T_s,1 = 0,5 R_s A_s,1Z₂. (6.87)

Соотношение принимают в указанных выше пределах.

Расчет производят для ряда нормальных сечений, расположенных по длине элемента, для арматуры, расположенной у каждой рассматриваемой грани элемента.

При действии крутящих моментов следует соблюдать конструктивные требования, приведенные в разделе 8.

Расчет на совместное действие крутящего и изгибающего моментов

6.2.39 Расчет по прочности элемента между пространственными сечениями производят согласно 6.2.37.

6.2.40 Расчет по прочности пространственного сечения производят из условия

, (6.88)

где Т — крутящий момент от внешней нагрузки в пространственном сечении;

T₀ — предельный крутящий момент, воспринимаемый пространственным сечением;

М — изгибающий момент от внешней нагрузки в нормальном сечении;

М₀ — предельный изгибающий момент, воспринимаемый нормальным сечением.

При расчете на совместное действие крутящего и изгибающего моментов рассматривают пространственное сечение с растянутой арматурой, расположенной у грани, растянутой от изгибающего момента, т.е. у грани, нормальной к плоскости действия изгибающего момента.

Крутящий момент Т от внешней нагрузки определяют в нормальном сечении, расположенном в середине длины проекции с вдоль продольной оси элемента. В этом же нормальном сечении определяют изгибающий момент М от внешней нагрузки.

Предельный крутящий момент Т₀ определяют согласно 6.2.38 и принимают равным правой части в условий (6.77) (равным T_sw + T_s) для рассматриваемого пространственного сечения.

Предельный изгибающий момент M₀ определяют согласно 6.2.10.

Допускается для определения крутящих моментов использовать условие (6.85). В этом случае крутящий момент Т = Т₁ и изгибающий момент М определяют в нормальных сечениях по длине элемента. В рассматриваемом нормальном сечении предельный крутящий момент принимают равным правой части условия (6.85) (T_sw,1 + T_s,1).

Предельный изгибающий момент М₀ определяют для того же нормального сечения, как было указано выше.

При совместном действии крутящих и изгибающих моментов следует соблюдать расчетные и конструктивные требования, приведенные в 6.2.38 и разделе 8.

Расчет на совместное действие крутящего момента и поперечной силы

6.2.41 Расчет по прочности элемента между пространственными сечениями производят из условия

, (6.89)

где T — крутящий момент от внешней нагрузки в нормальном сечении;

Т₀ — предельный крутящий момент, воспринимаемый элементом между пространственными сечениями и принимаемый равным правой части в условии (6.76);

Q — поперечная сила от внешней нагрузки в том же нормальном сечении;

Q₀ — предельная поперечная сила, воспринимаемая бетоном между наклонными сечениями и принимаемая равной правой части в условии (6.65).

6.2.42 Расчет по прочности пространственного сечения производят из условия (6.89), в котором принимают:

Т — крутящий момент от внешней нагрузки в пространственном сечении;

T₀ — предельный крутящий момент, воспринимаемый пространственным сечением;

Q — поперечная сила в наклонном сечении;

Q₀ — предельная поперечная сила, воспринимаемая наклонным сечением.

При расчете на совместное действие крутящего момента и поперечной силы рассматривают пространственное сечение с растянутой арматурой, расположенной у одной из граней, растянутой от поперечной силы, — т.е. у грани, параллельной плоскости действия поперечной силы.

Крутящий момент Т от внешней нагрузки определяют в нормальном сечении, расположенном в середине длины с вдоль продольной оси элемента. В том же нормальном сечении определяют поперечную силу Q от внешней нагрузки.

Предельный крутящий момент T₀ определяют согласно 6.2.38 и принимают равным правой части условия (6.77) (равным T_sw + T_s) для рассматриваемого пространственного сечения.

Предельную поперечную силу Q₀ определяют согласно 6.2.34 и принимают равной правой части условия (6.66). При этом середину длины проекции наклонного сечения на продольную ось элемента располагают в нормальном сечении, проходящем через середину длины проекции пространственного сечения на продольную ось элемента.

Допускается для определения крутящих моментов использовать условие (6.85), а для определения поперечных сил — условие (6.70). В этом случае крутящий момент Т = T₁ и поперечную силу Q = Q₁ от внешней нагрузки определяют в нормальных сечениях по длине элемента. В рассматриваемом нормальном сечении предельный крутящий момент Т₀принимают равным правой части условия (6.85) (равным Т_sw,1 + T_s,1), a предельную поперечную силу Q₀ в том же нормальном сечении принимают равной правой части условия (6.70) (равной Q_b,1 + Q_sw,l).

При совместном действии крутящих моментов и поперечных сил следует соблюдать расчетные и конструктивные требования, приведенные в 6.2.37, 6.2.32—6.2.35 и в разделе 8.

Расчет железобетонных элементов на местное сжатие

6.2.43 Расчет железобетонных элементов на местное сжатие (смятие) производят при действии сжимающей силы, приложенной на ограниченной площади нормально к поверхности железобетонного элемента. При этом учитывают повышенное сопротивление сжатию бетона в пределах грузовой площади (площади смятия) за счет объемного напряженного состояния бетона под грузовой площадью, зависящее от расположения грузовой площади на поверхности элемента.

При наличии косвенной арматуры в зоне местного сжатия учитывают дополнительное повышение сопротивления сжатию бетона под грузовой площадью за счет сопротивления косвенной арматуры.

Расчет элементов на местное сжатие при отсутствии косвенной арматуры производят согласно 6.2.44, а при наличии косвенной арматуры — согласно 6.2.45.

6.2.44 Расчет элементов на местное сжатие при отсутствии косвенной арматуры (рисунок 6.11) производят из условия

, (6.90)

где N — местная сжимающая сила от внешней нагрузки;

A_b,loc — площадь приложения сжимающей силы (площадь смятия);

R_b,loc — расчетное сопротивление бетона сжатию при местном действии сжимающей силы;

y — коэффициент, принимаемый равным 1,0 при равномерном и 0,75 при неравномерном распределении местной нагрузки по площади смятия.

а — вдали от краев элемента; б — по всей ширине элемента; в — у края (торца) элемента по всей его ширине; г — на углу элемента; д — у одного края элемента; е — вблизи одного края элемента

1 — элемент, на который действует местная нагрузка; 2 — площадь смятия А_b,loc;

3 — максимальная расчетная площадь А_b,max, 4 — центр тяжести площадей А_b,loc и A_b,max;

5 — минимальная зона армирования сетками, при которой косвенное армирование учитывается в расчете

Рисунок 6.11 — Схемы для расчета элементов на местное сжатие при расположении местной нагрузки

Значение R_b,loc определяют по формуле

R_b,loc = j_b R_b, (6.91)

где j_b — коэффициент, определяемый по формуле

, (6.92)

но принимаемый не более 2,5 и не менее 1,0.

В формуле (6.92):

A_b,max — максимальная расчетная площадь, устанавливаемая по следующим правилам:

центры тяжести площадей А_b,loc и A_b,max совпадают;

границы расчетной площади А_b,max отстоят от каждой стороны площади А_b,loc на расстоянии, равном соответствующему размеру этих сторон (рисунок 6.11).

6.2.45 Расчет элементов на местное сжатие при наличии косвенной арматуры в виде сварных сеток производят из условия

, (6.93)

где R_bs,loc — приведенное с учетом косвенной арматуры в зоне местного сжатия расчетное сопротивление бетона сжатию, определяемое по формуле

R_bs,loc = R_b,loc + 2j_s,xy R_s,xy m_s,xy. (6.94)

Здесь j_s,xy — коэффициент, определяемый по формуле

, (6.95)

A_b,loc,ef — площадь, заключенная внутри контура сеток косвенного армирования, считая по их крайним стержням, и принимаемая в формуле (6.92) не более A_b,max;

R_s,xy — расчетное сопротивление растяжению косвенной арматуры;

m_s,xy — коэффициент косвенного армирования, определяемый по формуле

, (6.96)

n_x, A_sx, l_x — число стержней, площадь сечения и длина стержня сетки, считая в осях крайних стержней, в направлении X;

n_y, A_sy, l_y — то же, в направлении Y;

s — шаг сеток косвенного армирования.

Значения R_b,loc, А_b,loc, y и N принимают согласно 6.2.44.

Значение местной сжимающей силы, воспринимаемое элементом с косвенным армированием (правая часть условия (6.93)), принимают не более удвоенного значения местной сжимающей силы, воспринимаемого элементом без косвенного армирования (правая часть условия (6.90)).

Косвенное армирование должно отвечать конструктивным требованиям, приведенным в 8.3.16.

Расчет железобетонных элементов на продавливание

Общие положения

6.2.46 Расчет на продавливание производят для плоских железобетонных элементов (плит) при действии на них (нормально к плоскости элемента) местных, концентрированно приложенных усилий — сосредоточенных силы и изгибающего момента.

При расчете на продавливание рассматривают расчетное поперечное сечение, расположенное вокруг зоны передачи усилий на элемент на расстоянии нормально к его продольной оси, по поверхности которого действуют касательные усилия от сосредоточенных силы и изгибающего момента.

Действующие касательные усилия по площади расчетного поперечного сечения должны быть восприняты бетоном с сопротивлением бетона осевому растяжению R_bt и расположенной по обе стороны от расчетного поперечного сечения на расстоянии поперечной арматурой с сопротивлением поперечной арматуры растяжению R_sw.

При действии сосредоточенной силы касательные усилия, воспринимаемые бетоном и арматурой, принимают равномерно распределенными по всей площади расчетного поперечного сечения. При действии изгибающего момента касательные усилия, воспринимаемые бетоном и поперечной арматурой, принимают с учетом неупругой работы бетона и арматуры. Допускается касательные усилия, воспринимаемые бетоном и арматурой, принимать линейно изменяющимися по длине расчетного поперечного сечения в направлении действия момента с максимальными касательными усилиями противоположного знака у краев расчетного поперечного сечения в этом направлении.

Расчет на продавливание при действии сосредоточенной силы и отсутствии поперечной арматуры производят согласно 6.2.47, при действии сосредоточенной силы и наличии поперечной арматуры — согласно 6.2.48, при действии сосредоточенных силы и изгибающего момента и отсутствии поперечной арматуры — согласно 6.2.49 и при действии сосредоточенных силы и изгибающего момента и наличии поперечной арматуры — согласно 6.2.50.

a — площадка приложения нагрузки внутри плоского элемента; б, в — то же, у края плоского элемента; г — при крестообразном расположении поперечной арматуры

1 — площадь приложения нагрузки; 2 — расчетный контур поперечного сечения;

2′ — второй вариант расположения расчетного контура; 3 — центр тяжести расчетного контура (место пересечения осей Х₁ и Y₁); 4 — центр тяжести площадки приложения нагрузки (место пересечения осей Х и Y); 5 — поперечная арматура; 6 — контур расчетного поперечного сечения без учета в расчете поперечной арматуры; 7 — граница (край) плоского элемента

Рисунок 6.12 — Схема расчетных контуров поперечного сечения при продавливании

Расчетный контур поперечного сечения принимают: при расположении площадки передачи нагрузки внутри плоского элемента — замкнутым и расположенным вокруг площадки передачи нагрузки (рисунок 6.12, а, г), при расположении площадки передачи нагрузки у края или угла плоского элемента — в виде двух вариантов: замкнутым, расположенным вокруг площадки передачи нагрузки, и незамкнутым, следующим от краев плоского элемента (рисунок 6.12, б, в), в этом случае учитывают наименьшую несущую способность при двух вариантах расположения расчетного контура поперечного сечения.

При действии момента М_lос в месте приложения сосредоточенной нагрузки половину этого момента учитывают при расчете на продавливание, а другую половину учитывают при расчете по нормальным сечениям по ширине сечения, включающего ширину площадки передачи нагрузки и высоту сечения плоского элемента по обе стороны от площадки передачи нагрузки.

При действии сосредоточенных моментов и силы в условиях прочности соотношение между действующими сосредоточенными моментами М, учитываемыми при продавливании, и предельными M_ult принимают не более соотношения между действующим сосредоточенным усилием F и предельным F_ult.

Расчет элементов на продавливание при действии сосредоточенной силы

6.2.47 Расчет элементов без поперечной арматуры на продавливание при действии сосредоточенной силы производят из условия

F £ F_b,ult, (⁶-97)

где F — сосредоточенная сила от внешней нагрузки;

F_b,ult — предельное усилие, воспринимаемое бетоном.

Усилие F_b,ult определяют по формуле

F_b,ult = R_bt A_b, (6.98)

где А_b — площадь расчетного поперечного сечения, расположенного на расстоянии 0,5 h₀ от границы площади приложения сосредоточенной силы F с рабочей высотой сечения h₀(рисунок 6.13).

1 — расчетное поперечное сечение; 2 — контур расчетного поперечного сечения;

3 — контур площадки приложения нагрузки

Рисунок 6.13 — Схема для расчета железобетонных элементов без поперечной арматуры на продавливание

Площадь А_b определяют по формуле

A_b = u h₀, (6.99)

где u — периметр контура расчетного поперечного сечения;

h₀ — приведенная рабочая высота сечения h₀ = 0,5 (h_0x + h_0y),

здесь h_0x и h_0y — рабочая высота сечения для продольной арматуры, расположенной в направлении осей Х и Y.

6.2.48 Расчет элементов с поперечной арматурой на продавливание при действии сосредоточенной силы (рисунок 6.14) производят из условия

F £ F_b,ult + F_sw,ult, (6.100)

где F_sw,ult — предельное усилие, воспринимаемое поперечной арматурой при продавливании;

F_b,ult — предельное усилие, воспринимаемое бетоном, определяемое согласно 6.2.47.

1 — расчетное поперечное сечение; 2 — контур расчетного поперечного сечения;

3 — границы зоны, в пределах которых в расчете учитывается поперечная арматура;

4 — контур расчетного поперечного сечения без учета в расчете поперечной арматуры;

5 — контур площадки приложения нагрузки

Рисунок 6.14 — Схема для расчета железобетонных плит с вертикальной, равномерно распределенной поперечной арматурой на продавливание

Усилие F_sw,ult, воспринимаемое поперечной арматурой, нормальной к продольной оси элемента и расположенной равномерно вдоль контура расчетного поперечного сечения, определяют по формуле

F_sw,ult = 0,8 q_sw u, (6.101)

где q_sw — усилие в поперечной арматуре на единицу длины контура расчетного поперечного сечения, расположенной в пределах расстояния 0,5h₀ по обе стороны от контура расчетного сечения

; (6.102)

A_sw — площадь сечения поперечной арматуры с шагом s_w, расположенная в пределах расстояния 0,5 h₀ по обе стороны от контура расчетного поперечного сечения по периметру контура расчетного поперечного сечения;

u — периметр контура расчетного поперечного сечения, определяемый согласно 6.2.47.

При расположении поперечной арматуры не равномерно по контуру расчетного поперечного сечения, а сосредоточенно у осей площадки передачи нагрузки (крестообразное расположение поперечной арматуры) периметр контура u для поперечной арматуры принимают по фактическим длинам участков расположения поперечной арматурыL_swx и L_swy по расчетному контуру продавливания (рисунок 6.12, г).

Значение F_b,ult + F_sw,ult принимают не более 2F_b,ult. Поперечную арматуру учитывают в расчете при F_sw,ult не менее 0,25F_b,ult.

За границей расположения поперечной арматуры расчет на продавливание производят согласно 6.2.47, рассматривая контур расчетного поперечного сечения на расстоянии 0,5 h₀от границы расположения поперечной арматуры (рисунок 6.14). При сосредоточенном расположении поперечной арматуры по осям площадки передачи нагрузки, кроме этого, расчетный контур поперечного сечения бетона принимают по диагональным линиям, следующим от края расположения поперечной арматуры (рисунок 6.12, г).

Поперечная арматура должна удовлетворять конструктивным требованиям, приведенным в 8.3.9-8.3.17.

Расчет элементов на продавливание при действии сосредоточенных силы и изгибающего момента

6.2.49 Расчет элементов без поперечной арматуры на продавливание при совместном действии сосредоточенных силы и изгибающего момента (рисунок 6.13) производят из условия

, (6.103)

где F — сосредоточенная сила от внешней нагрузки;

М — сосредоточенный изгибающий момент от внешней нагрузки, учитываемый при расчете на продавливание (6.2.46);

F_b,ult и M_b,ult — предельные сосредоточенные сила и изгибающий момент, которые могут быть восприняты бетоном в расчетном поперечном сечении при их раздельном действии.

В железобетонном каркасе зданий с плоскими перекрытиями сосредоточенный изгибающий момент М_loc равен суммарному изгибающему моменту в сечениях верхней и нижней колонн, примыкающих к перекрытию в рассматриваемом узле.

Предельную силу F_b,ult определяют согласно 6.2.47.

Предельный изгибающий момент M_b,ult определяют по формуле

M_b,ult = R_bt W_b h₀, (6.104)

где W_b — момент сопротивления расчетного контура поперечного сечения, определяемый согласно 6.2.47.

При действии изгибающих моментов в двух взаимно перпендикулярных плоскостях расчет производят из условия

, (6.105)

где F, M_x и M_y — сосредоточенные сила и изгибающие моменты в направлениях осей X и Y, учитываемые при расчете на продавливание (6.2.46), от внешней нагрузки;

F_b,ult, M_bx,ult, M_by,ult — предельные сосредоточенные сила и изгибающие моменты в направлениях осей Х и Y, которые могут быть восприняты бетоном в расчетном поперечном сечении при их раздельном действии.

Усилие F_b,ult определяют согласно 6.2.47.

Усилия M_bx,ult и M_by,ult определяют согласно указаниям, приведенным выше, при действии момента соответственно в плоскости оси Х и в плоскости оси Y.

При расположении сосредоточенной силы внецентренно относительно центра тяжести контура расчетного поперечного сечения значения изгибающих сосредоточенных моментов от внешней нагрузки определяют с учетом дополнительного момента от внецентренного приложения сосредоточенной силы относительно центра тяжести контура расчетного поперечного сечения.

6.2.50 Расчет прочности элементов с поперечной арматурой на продавливание при действии сосредоточенных силы и изгибающего момента (рисунок 6.14) производят из условия

, (6.106)

где F и M — по 6.2.48;

F_b,ult и M_b,ult — предельные сосредоточенные сила и изгибающий момент, которые могут быть восприняты бетоном в расчетном поперечном сечении при их раздельном действии;

F_sw,ult и M_sw,ult — предельные сосредоточенные сила и изгибающий момент, которые могут быть восприняты поперечной арматурой при их раздельном действии.

Усилия F_b,ult, M_b,ult и F_sw,ult определяют согласно 6.2.48 и 6.2.49.

Усилие M_sw,ult, воспринимаемое поперечной арматурой, нормальной к плоскости элемента и расположенной равномерно вдоль контура расчетного сечения, определяют по формуле

M_sw,ult = 0,8 q_sw W_sw, (6.107)

где q_sw и W_sw — определяют согласно 6.2.48 и 6.2.52.

При действии сосредоточенных изгибающих моментов в двух взаимно перпендикулярных плоскостях расчет производят из условия

, (6.108)

где F, М_х и М_у — по 6.2.49;

F_b,ult, M_bx,ult и M_by,ult — предельные сосредоточенные сила и изгибающие моменты в направлениях осей X и Y, которые могут быть восприняты бетоном в расчетном поперечном сечении при их раздельном действии;

F_sw,ult, M_sw,x,ult и M_sw,y,ult — предельные сосредоточенные сила и изгибающие моменты в направлениях осей X и Y, которые могут быть восприняты поперечной арматурой при их раздельном действии.

Усилия F_b,ult, M_bx,ult, M_by,ult и F_sw,ult определяют согласно указаниям 6.2.48 и 6.2.49.

Усилия M_sw,x,ult и M_sw,y,ult определяют согласно указаниям, приведенным выше, при действии изгибающего момента соответственно в направлении оси X и оси Y.

Значения F_b,ult + F_sw,ult, M_b,ult + M_sw,ult, M_bx,ult + M_sw,x,ult, M_by,ult + M_sw,y,ult в условиях (6.106) и (6.108) принимают не более соответственно 2F_b,ult, 2M_b,ult, 2M_bx,ult, 2M_by,ult.

Поперечная арматура должна отвечать конструктивным требованиям, приведенным в 8.3.9-8.3.17.

6.2.51 В общем случае значения момента сопротивления расчетного контура бетона при продавливании W_bx(y) в направлениях взаимно перпендикулярных осей X и Y определяют по формуле

, (6.109)

где I_bx(y) — момент инерции расчетного контура относительно осей Х₁ и Y₁, проходящих через его центр тяжести (рисунок 6.12);

у(х)_max — максимальное расстояние от расчетного контура до его центра тяжести.

Значение момента инерции I_bx(y) определяют как сумму моментов инерции I_bx(y)i отдельных участков расчетного контура поперечного сечения относительно центральных осей, проходящих через центр тяжести расчетного контура.

Положение центра тяжести расчетного контура относительно выбранной оси определяют по формуле

, (6.110)

где L_i — длина отдельного участка расчетного контура;

x_i(y_i)₀ — расстояние от центров тяжести отдельных участков расчетного контура до выбранных осей.

Для замкнутого прямоугольного контура (рисунок 6.12, а, г) с длиной участков L_x и L_y в направлении осей Х и Y центр тяжести расположен в месте пересечения осей симметрии контура.

Значение момента инерции расчетного контура определяют по формуле

I_bx(y) = I_bx(y)1 + I_bx(y)2, (6.111)

где I_bx(y)1,2 — момент инерции участков контура длиной L_x и L_y относительно осей Y₁ и Х₁, совпадающих с осями Y и X.

Значения I_bx(y)1,2 определяют по формулам (6.112) и (6.113), принимая условно ширину каждого участка контура длиной L_x и L_y, равной единице:

; (6.112)

. (6.113)

Значения W_bx(y) определяют по формуле

(6.114)

или

. (6.115)

Для незамкнутого расчетного контура, состоящего из трех прямолинейных участков длинойL_x и L_y (рисунок 6.12, в), например, при расположении площадки передачи нагрузки (колонны) у края плоского элемента (плиты перекрытия), положение центра тяжести расчетного контура в направлении оси X определяют по формуле

, (6.116)

а в направлении оси Y центр тяжести расположен по оси симметрии расчетного контура.

Значения момента инерции расчетного контура относительно центральных осей Y₁ и Х₁определяют по формуле (6.111).

Значения I_bx1 и I_bx2 определяют по формулам:

; (6.117)

I_bx2 = L_y (L_x — x₀)². (6.118)

Значения I_by1 и I_by2 определяют по формулам:

; (6.119)

. (6.120)

Значения W_bx и W_by определяют по формулам:

и ; (6.121)

. (6.122)

При расчете принимают наименьшие значения моментов сопротивления W_bx.

Для незамкнутого расчетного контура, состоящего из двух прямолинейных участков длинойL_x и L_y (рисунок 6.12, б), например при расположении площадки передачи нагрузки (колонны) вблизи угла плоского элемента (плиты перекрытия), положение центра тяжести расчетного контура в направлении осей X и Y определяют по формуле

. (6.123)

Значения момента инерции расчетного контура относительно центральных осей Y₁ и Х₁определяют по формуле (6.20).

Значения I_bx(y)1 и I_bx(y)2 определяют по формулам:

; (6.124)

I_bx2 = L_y (L_x — x₀)²; (6.125)

I_byl = L_x (L_y — y₀)²; (6.126)

. (6.127)

Значения W_bx и W_by определяют по формулам:

и ; (6.128)

и ; (6.129)

При расчете принимают наименьшие значения моментов сопротивления W_bx и W_by.

6.2.52 Значения моментов сопротивления поперечной арматуры при продавливании W_sw,x(y)в том случае, когда поперечная арматура расположена равномерно вдоль расчетного контура продавливания в пределах зоны, границы которой отстоят на расстоянии в каждую сторону от контура продавливания бетона (рисунок 6.14), принимают равными соответствующим значениям W_bx и W_by.

При расположении поперечной арматуры в плоском элементе сосредоточенно по осям грузовой площадки, например, по оси колонн (крестообразное расположение поперечной арматуры в перекрытии), моменты сопротивления поперечной арматуры определяют по тем же правилам, что и моменты сопротивления бетона, принимая соответствующую фактическую длину ограниченного участка расположения поперечной арматуры по расчетному контуру продавливания L_swx и L_swy (рисунок 6.12, г).

7 РАСЧЕТ ЭЛЕМЕНТОВ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ВТОРОЙ ГРУППЫ

7.1 ОБЩИЕ ПОЛОЖЕНИЯ

7.1.1 Расчеты по предельным состояниям второй группы включают:

— расчет по раскрытию трещин;

— расчет по деформациям.

7.1.2 Расчет по образованию трещин производят для проверки необходимости расчета по раскрытию трещин, а также для проверки необходимости учета трещин при расчете по деформациям.

7.1.3 При расчете по предельным состояниям второй группы нагрузки принимают с коэффициентом надежности по нагрузке g_f = 1,0.

7.2 РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО РАСКРЫТИЮ ТРЕЩИН

Общие положения

7.2.1 Расчет железобетонных элементов по раскрытию трещин производят в тех случаях, когда соблюдается условие

М > М_crc, (7.1)

где М — изгибающий момент от внешней нагрузки относительно оси, нормальной к плоскости действия момента и проходящей через центр тяжести приведенного поперечного сечения элемента;

М_crc — изгибающий момент, воспринимаемый нормальным сечением элемента при образовании трещин, определяемый согласно (7.6).

Для центрально-растянутых элементов ширину раскрытия трещин определяют при соблюдении условия

N > N_crc, (7.2)

где N — продольное растягивающее усилие от внешней нагрузки;

N_crc — продольное растягивающее усилие, воспринимаемое элементом при образовании трещин, определяемое согласно 7.2.10.

7.2.2 Расчет железобетонных элементов производят по непродолжительному и продолжительному раскрытию трещин.

Непродолжительное раскрытие трещин определяют от совместного действия постоянных и временных (длительных и кратковременных) нагрузок, продолжительное — только от постоянных и временных длительных нагрузок (4.2.4).

7.2.3 Расчет по раскрытию трещин производят из условия

a_crc £ a_crc,ult, (7.3)

где а_crc — ширина раскрытия трещин от действия внешней нагрузки, определяемая согласно 7.2.4, 7.2.12—7.2.14;

a_crc,ult — предельно допустимая ширина раскрытия трещин.

Значения a_crc,ult принимают равными:

а) из условия обеспечения сохранности арматуры:

0,3 мм — при продолжительном раскрытии трещин;

0,4 мм — при непродолжительном раскрытии трещин;

б) из условия ограничения проницаемости конструкций:

0,2 мм — при продолжительном раскрытии трещин;

0,3 мм — при непродолжительном раскрытии трещин.

7.2.4 Ширину раскрытия трещин а_crc определяют исходя из взаимных смещений растянутой арматуры и бетона по обе стороны трещины на уровне оси арматуры и принимают:

— при продолжительном раскрытии

а_crc = а_crc,1; (7.4)

— при непродолжительном раскрытии

а_crc = а_crc,1 + а_crc,2 — а_crc,3; (7.5)

где а_crc,1 — ширина раскрытия трещин от продолжительного действия постоянных и временных длительных нагрузок;

а_crc,2 — ширина раскрытия трещин от непродолжительного действия постоянных и временных (длительных и кратковременных) нагрузок;

а_crc,3 — ширина раскрытия трещин от непродолжительного действия постоянных и временных длительных нагрузок.

Значения а_crc,1, а_crc,2 и а_crc,3 определяют с учетом влияния продолжительности действия соответствующей нагрузки.

Определение момента образования трещин, нормальных к продольной оси элемента

7.2.5 Изгибающий момент М_crc при образовании трещин определяют согласно 7.2.6 или по деформационной модели согласно 7.2.11.

7.2.6 Определение момента образования трещин производят с учетом неупругих деформаций растянутого бетона согласно 7.2.7.

Допускается момент образования трещин определять без учета неупругих деформаций растянутого бетона по 7.2.8. Если при этом условия (7.3) и (7.24) не удовлетворяются, то момент образования трещин следует определять с учетом неупругих деформаций растянутого бетона.

7.2.7 Момент образования трещин с учетом неупругих деформаций растянутого бетона определяют с учетом следующих положений:

— сечения после деформирования остаются плоскими;

— эпюру напряжений в сжатой зоне бетона принимают треугольной формы, как для упругого тела (рисунок 7.1);

— эпюру напряжений в растянутой зоне бетона принимают трапециевидной формы с напряжениями, не превышающими расчетных значений сопротивления бетона растяжениюR_bt,ser;

— относительную деформацию крайнего растянутого волокна бетона принимают равной ее предельному значению e_bt,ult при кратковременном действии нагрузки (6.2.31); при двухзначной эпюре деформаций в сечении элемента e_bt,ult = 0,00015;

— напряжения в арматуре принимают в зависимости от относительных деформаций как для упругого тела.

7.2.8 Момент образования трещин без учета неупругих деформаций растянутого бетона определяют как для сплошного упругого тела по формуле

M_сrc = R_bt,ser ± Ne_x, (7.6)

где W — момент сопротивления приведенного сечения для крайнего растянутого волокна бетона, определяемый согласно 7.2.9;

е_х — расстояние от точки приложения продольной силы N (расположенной в центре тяжести приведенного сечения элемента) до ядровой точки, наиболее удаленной от растянутой зоны, трещинообразование которой проверяется.

В формуле (7.6) знак «плюс» принимают при сжимающей продольной силе N, «минус» — при растягивающей силе.

7.2.9 Момент сопротивления W и расстояние е_х определяют по формулам:

; (7.7)

, (7.8)

где I_red — момент инерции приведенного поперечного сечения относительно его центра тяжести

; (7.9)

I, I_s, I‘_s — моменты инерции сечений соответственно бетона, растянутой и сжатой арматуры;

A_red — площадь приведенного поперечного сечения элемента, определяемая по формуле

A_red = А + A_sa + A’_sa; (7.10)

a — коэффициент приведения арматуры к бетону

;

y_t — расстояние от наиболее растянутого волокна бетона до центра тяжести приведенного поперечного сечения элемента

,

здесь S_t,red — статический момент площади приведенного поперечного сечения элемента относительно наиболее растянутого волокна бетона.

Допускается момент сопротивления W определять без учета арматуры.

1 — уровень центра тяжести приведенного поперечного сечения

Рисунок 7.1 — Схема напряженно-деформированного состояния сечения элемента при проверке образования трещин при действии изгибающего момента (а), изгибающего момента и продольной силы (б)

В этом случае значения I_s, I‘_s, A_s, A‘_s в формулах (7.9) и (7.10) принимают равными нулю.

Для изгибаемых элементов прямоугольного сечения момент сопротивления W без учета арматуры определяют по формуле

. (7.11)

7.2.10 Усилие N_crc при образовании трещин в центрально-растянутых элементах определяют по формуле

N_crc = А_rеd R_bt,ser. (7.12)

7.2.11 Определение момента образования трещин на основе нелинейной деформационной модели производят исходя из общих положений, приведенных в 5.1.22 и 6.2.2—6.2.31, но с учетом работы бетона в растянутой зоне нормального сечения, определяемой диаграммой состояния растянутого бетона согласно 5.1.20. Расчетные характеристики материалов принимают для предельных состояний второй группы.

Значение М_crc определяют из решения системы уравнений, представленных в 6.2.2—6.2.31, принимая относительную деформацию бетона e_bt,max у растянутой грани элемента от действия внешней нагрузки равной предельному значению относительной деформации бетона при растяжении e_bt,ult, определяемому согласно указаниям 6.2.31.

Расчет ширины раскрытия трещин, нормальных к продольной оси элемента

7.2.12 Ширину раскрытия нормальных трещин определяют по формуле

, (7.13)

где s_s — напряжение в продольной растянутой арматуре в нормальном сечении с трещиной от соответствующей внешней нагрузки, определяемое согласно 7.2.13;

l_s — базовое (без учета влияния вида поверхности арматуры) расстояние между смежными нормальными трещинами;

y_s — коэффициент, учитывающий неравномерное распределение относительных деформаций растянутой арматуры между трещинами; допускается принимать коэффициент y_s=1, если при этом условие (7.3) не удовлетворяется, значение y_s следует определять по формуле (7.23);

j₁ — коэффициент, учитывающий продолжительность действия нагрузки, принимаемый равным:

1,0 — при непродолжительном действии нагрузки;

1,4 — при продолжительном действии нагрузки;

j₂ — коэффициент, учитывающий профиль продольной арматуры, принимаемый равным:

0,5 — для арматуры периодического профиля;

0,8 — для гладкой арматуры;

j₃ — коэффициент, учитывающий характер нагружения, принимаемый равным:

1,0 — для элементов изгибаемых и внецентренно сжатых;

1,2 — для растянутых элементов.

7.2.13 Значения напряжения s_s в растянутой арматуре изгибаемых элементов определяют по формуле

, (7.14)

где I_red, у_с — момент инерции и расстояние от сжатой грани до центра тяжести приведенного поперечного сечения элемента, определяемые с учетом площади сечения только сжатой зоны бетона, площадей сечения растянутой и сжатой арматуры согласно 7.3.11, принимая в соответствующих формулах значения коэффициента приведения арматуры к бетону a_s2 = a_s1.

Для изгибаемых элементов у_с = х (рисунок 7.2), где х — высота сжатой зоны бетона, определяемая согласно 7.3.12 при a_s2 = a_s1.

Значение коэффициента приведения арматуры к бетону a_s1 определяют по формуле

, (7.15)

где E_b,red — приведенный модуль деформации сжатого бетона, учитывающий неупругие деформации сжатого бетона и определяемый по формуле

. (7.16)

Относительную деформацию бетона e_b1,red принимают равной 0,0015.

Допускается напряжение s_s определять по формуле

, (7.17)

где z_s — расстояние от центра тяжести растянутой арматуры до точки приложения равнодействующей усилий в сжатой зоне элемента.

Для элементов прямоугольного поперечного сечения при отсутствии (или без учета) сжатой арматуры значение z_s определяют по формуле

. (7.18)

Для элементов прямоугольного, таврового (с полкой в сжатой зоне) и двутаврового поперечного сечения допускается значение z_s принимать равным 0,8h₀.

При действии изгибающего момента М и продольной силы N напряжение s_s в растянутой арматуре определяют по формуле

, (7.19)

где A_red, у_с — площадь приведенного поперечного сечения элемента и расстояние от наиболее сжатого волокна бетона до центра тяжести приведенного сечения, определяемые по общим правилам расчета геометрических характеристик сечений упругих элементов с учетом площади сечения только сжатой зоны бетона, площадей сечения растянутой и сжатой арматуры, принимая коэффициент приведения арматуры к бетону a_s1.

1 — уровень центра тяжести приведенного поперечного сечения

Рисунок 7.2 — Схема напряженно-деформированного состояния элемента с трещинами при действии изгибающего момента (а, б), изгибающего момента и продольной силы (в)

Допускается напряжение s_s определять по формуле

, (7.20)

где e_s — расстояние от центра тяжести растянутой арматуры до точки приложения продольной силы N с учетом эксцентриситета, равного .

Для элементов прямоугольного сечения при отсутствии (или без учета) сжатой арматуры значение z_s допускается определять по формуле 7.18, в которой х принимается равным высоте сжатой зоны бетона с учетом влияния продольной силы, определяемой согласно 7.3.12, принимая коэффициент приведения арматуры к бетону a_s2 = a_s1.

Для элементов прямоугольного, таврового (с полкой в сжатой зоне) и двутаврового поперечного сечения допускается значение z_s принимать равным 0,7h₀.

В формулах (7.19) и (7.20) знак «плюс» принимают при растягивающей, а знак «минус» — при сжимающей продольной силе.

Напряжения s_s не должны превышать R_s,ser.

7.2.14 Значения базового расстояния между трещинами l_s определяют по формуле

(7.21)

и принимают не менее 10d_s и 10 см и не более 40d_s и 40 см (для элементов с рабочей высотой поперечного сечения не более 1 м).

Здесь А_bt — площадь сечения растянутого бетона.

Значения А_bt определяют по высоте растянутой зоны бетона x, используя правила расчета момента образования трещин согласно указаниям 7.2.5—7.2.11.

В любом случае значение А_bt принимают равным площади сечения при ее высоте в пределах не менее 2а и не более 0,5h.

7.2.15 Значения коэффициента y_s определяют по формуле

, (7.22)

где s_s,crc — напряжение в продольной растянутой арматуре в сечении с трещиной сразу после образования нормальных трещин, определяемое по указаниям 7.2.13;

s_s — то же, при действии рассматриваемой нагрузки.

Для изгибаемых элементов значение коэффициента y_s допускается определять по формуле

, (7.23)

где М_crc — по (7.6).

7.3 РАСЧЕТ ЭЛЕМЕНТОВ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ ПО ДЕФОРМАЦИЯМ

Общие положения

7.3.1 Расчет элементов железобетонных конструкций по деформациям производят с учетом эксплуатационных требований, предъявляемых к конструкциям.

Расчет по деформациям следует производить на действие:

постоянных, временных длительных и кратковременных нагрузок (4.2.4) при ограничении деформаций технологическими или конструктивными требованиями;

постоянных и временных длительных нагрузок при ограничении деформаций эстетическими требованиями.

7.3.2 Значения предельно допустимых деформаций элементов принимают согласно СНиП 2.01.07 и нормативным документам на отдельные виды конструкций.

Расчет железобетонных элементов по прогибам

7.3.3 Расчет железобетонных элементов по прогибам производят из условия

f £ f_ult, (7.24)

где f — прогиб железобетонного элемента от действия внешней нагрузки;

f_ult — значение предельно допустимого прогиба железобетонного элемента.

Прогибы железобетонных конструкций определяют по общим правилам строительной механики в зависимости от изгибных, сдвиговых и осевых деформационных характеристик железобетонного элемента в сечениях по его длине (кривизн, углов сдвига и т.д.).

В тех случаях, когда прогибы железобетонных элементов в основном зависят от изгибных деформаций, значения прогибов определяют по кривизнам элементов согласно 7.3.4—7.3.6 или по жесткостным характеристикам согласно 7.3.5 и 7.3.16.

При действии постоянных, длительных и кратковременных нагрузок прогиб балок или плит во всех случаях не должен превышать ¹/₁₅₀ пролета и ¹/₇₅ вылета консоли.

7.3.4 Прогиб железобетонных элементов, обусловленный деформацией изгиба, определяют по формуле

, (7.25)

где — изгибающий момент в сечении х от действия единичной силы, приложенной по направлению искомого перемещения элемента в сечении по длине пролета l, для которого определяют прогиб;

— полная кривизна элемента в сечении х от внешней нагрузки, при которой определяют прогиб.

В общем случае для железобетонных изгибаемых элементов вычисление прогиба производят путем разбиения элемента на ряд участков, определения кривизны на границах этих участков (с учетом отсутствия или наличия трещин и знака кривизны) и перемножения эпюр моментов и кривизны по длине элемента при линейном распределение кривизны в пределах каждого участка. В этом случае прогиб в середине пролета элемента определяют по формуле

, (7.26)

где , — кривизна элемента соответственно на левой и правой опорах;

, — кривизны элемента в симметрично расположенных сечениях i и i‘ (i = i‘) соответственно слева и справа от оси симметрии (середины пролета);

— кривизна элемента в середине пролета;

n — четное число равных участков, на которые разделяют пролет, принимаемое не менее 6;

l — пролет элемента.

В формулах (7.25), (7.26) кривизны определяют по указаниям 7.3.7—7.3.16 соответственно для участков без трещин и с трещинами. Знак принимают в соответствии с эпюрой кривизны.

7.3.5 Для изгибаемых элементов постоянного по длине элемента сечения, не имеющих трещин, прогибы определяют по общим правилам строительной механики с использованием жесткости поперечного сечения, определяемой по формуле (7.31).

7.3.6 Для изгибаемых элементов постоянного по длине элемента сечения, имеющих трещины, на каждом участке, в пределах которого изгибающий момент не меняет знак, кривизну допускается вычислять для наиболее напряженного сечения, принимая ее для остальных сечений такого участка изменяющейся пропорционально значениям изгибающего момента.

Для свободно опертых или консольных элементов максимальный прогиб определяют по формуле

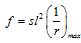
, (7.27)

где s — коэффициент, зависящий от расчетной схемы элемента и вида нагрузки, определяемый по правилам строительной механики; при действии равномерно распределенной нагрузки значение s принимают равным:

— для свободно опертой балки и

— для консольной балки;

— полная кривизна в сечении с наибольшим изгибающим моментом от нагрузки, при которой определяют прогиб, вычисляемая согласно 7.3.7—7.3.16.

Определение кривизны железобетонных элементов

Общие положения

7.3.7 Кривизну изгибаемых, внецентренно сжатых и внецентренно растянутых элементов для вычисления их прогибов определяют:

а) для элементов или участков элемента, где в растянутой зоне не образуются нормальные к продольной оси трещины, — согласно 7.3.8, 7.3.10;

б) для элементов или участков элемента, где в растянутой зоне имеются трещины, — согласно 7.3.8, 7.3.9 и 7.3.11.

Элементы или участки элементов рассматривают без трещин, если трещины не образуются (т.е. условие (7.1) не выполняется) при действии полной нагрузки, включающей постоянную, временную длительную и кратковременную нагрузки.

Кривизну железобетонных элементов с трещинами и без трещин можно также определять на основе деформационной модели согласно 7.3.17.

7.3.8 Полную кривизну изгибаемых, внецентренно сжатых и внецентренно растянутых элементов определяют по формулам:

для участков без трещин в растянутой зоне

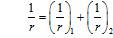
; (7.28)

для участков с трещинами в растянутой зоне

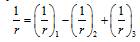
; (7.29)

В формуле (7.28):

, — кривизны соответственно от непродолжительного действия кратковременных нагрузок и от продолжительного действия постоянных и временных длительных нагрузок.

В формуле (7.29):

— кривизна от непродолжительного действия всей нагрузки, на которую производят расчет по деформациям;

— кривизна от непродолжительного действия постоянных и временных длительных нагрузок;

— кривизна от продолжительного действия постоянных и временных длительных нагрузок.

Кривизны , и определяют согласно указаниям 7.3.9.

7.3.9 Кривизну железобетонных элементов от действия соответствующих нагрузок (7.3.8) определяют по формуле

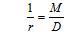
, (7.30)

где М — изгибающий момент от внешней нагрузки (с учетом момента от продольной силы N) относительно оси, нормальной к плоскости действия изгибающего момента и проходящей через центр тяжести приведенного поперечного сечения элемента;

D — изгибная жесткость приведенного поперечного сечения элемента, определяемая по формуле

D = E_b1I_red, (7.31)

где E_b1 — модуль деформации сжатого бетона, определяемый в зависимости от продолжительности действия нагрузки;

I_red — момент инерции приведенного поперечного сечения относительно его центра тяжести, определяемый с учетом наличия или отсутствия трещин.

Значения модуля деформации бетона E_b1 и момента инерции приведенного сечения I_red для элементов без трещин в растянутой зоне и с трещинами определяют соответственно по указаниям 7.3.10 и 7.3.11.

Жесткость железобетонного элемента на участке без трещин в растянутой зоне

7.3.10 Жесткость железобетонного элемента D на участке без трещин определяют по формуле (7.31).

Момент инерции I_red приведенного поперечного сечения элемента относительно его центра тяжести определяют как для сплошного тела по общим правилам сопротивления упругих элементов с учетом всей площади сечения бетона и площадей сечения арматуры с коэффициентом приведения арматуры к бетону a

I_red = I + I_s a + I’_s a, (7.32)

где I — момент инерции бетонного сечения относительно центра тяжести приведенного поперечного сечения элемента;

I_s, I‘_s — моменты инерции площадей сечения соответственно растянутой и сжатой арматуры относительно центра тяжести приведенного поперечного сечения элемента;

I_s = A_s (h₀ — y_c)²; (7.33)

I’_s = A’_s (y_c — a’)²; (7.34)

a — коэффициент приведения арматуры к бетону

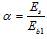
; (7.35)

у_с — расстояние от наиболее сжатого волокна бетона до центра тяжести приведенного поперечного сечения элемента.

Значения I и у_с определяют по общим правилам расчета геометрических характеристик сечений упругих элементов.

Допускается определять момент инерции I_red без учета арматуры.

В этом случае для прямоугольного сечения

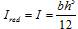
. (7.36)

Значения модуля деформации бетона в формулах (7.31), (7.35) принимают равными:

при непродолжительном действии нагрузки

Е_b1 = 0,85 E_b; (7.37)

при продолжительном действии нагрузки

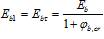
, (7.38)

где j_b,cr — принимают по таблице 5.5.

Жесткость железобетонного элемента на участке с трещинами в растянутой зоне

7.3.11 Жесткость железобетонного элемента на участках с трещинами в растянутой зоне определяют с учетом следующих положений:

— сечения после деформирования остаются плоскими;

— напряжения в бетоне сжатой зоны определяют как для упругого тела;

— работу растянутого бетона в сечении с нормальной трещиной не учитывают;

— работу растянутого бетона на участке между смежными нормальными трещинами учитывают посредством коэффициента y_s.

Жесткость железобетонного элемента D на участках с трещинами определяют по формуле (7.31) и принимают не более жесткости без трещин.

Значения модуля деформации сжатого бетона Е_b1 принимают равными значениям приведенного модуля деформации E_b,red, определяемым по формуле (5.9) при расчетных значениях сопротивления бетона R_bt,ser для соответствующих нагрузок (непродолжительного и продолжительного действия).

Момент инерции приведенного поперечного сечения элемента I_red относительно его центра тяжести определяют по общим правилам сопротивления упругих элементов с учетом площади сечения бетона только сжатой зоны, площадей сечения сжатой арматуры с коэффициентом приведения арматуры к бетону a_s1 и растянутой арматуры с коэффициентом приведения арматуры к бетону a_s2

I_red = I_b + I_s a_s2 + I’_s a_s1, (7.39)

где I_b, I_s, I‘_s — моменты инерции площадей сечения соответственно сжатой зоны бетона, растянутой и сжатой арматуры относительно центра тяжести приведенного без учета бетона растянутой зоны поперечного сечения.

Значения I_s и I‘_s определяют по формулам (7.33) и (7.34), принимая вместо у_с значение у_cm, равное расстоянию от наиболее сжатого волокна бетона до центра тяжести приведенного (с коэффициентами приведения a_s1 и a_s2) поперечного сечения без учета бетона растянутой зоны (рисунок 7.3); для изгибаемых элементов

y_cm = x_m,

где x_m — средняя высота сжатой зоны бетона, учитывающая влияние работы растянутого бетона между трещинами и определяемая согласно 7.3.12 (рисунок 7.3).

Значения I_b и у_cm определяют по общим правилам расчета геометрических характеристик сечений упругих элементов.

Значения коэффициентов приведения арматуры к бетону a_s1 и a_s2 определяют по 7.3.14.

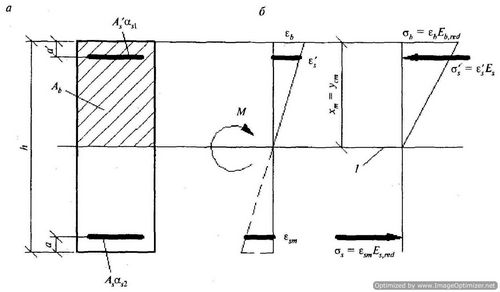
1 — уровень центра тяжести приведенного без учета растянутой зоны бетона поперечного сечения

Рисунок 7.3 — Приведенное поперечное сечение (а) и схема напряженно-деформированного состояния элемента с трещинами (б) для расчета его по деформациям при действии изгибающего момента

7.3.12 Для изгибаемых элементов положение нейтральной оси (средняя высота сжатой зоны бетона) определяют из уравнения

S_b0 = a_s2S_s0 — a_s1S’_s0, (7.40)

где S_b0, S_s0 и S‘_s0 — статические моменты соответственно сжатой зоны бетона, растянутой и сжатой арматуры относительно нейтральной оси.

Для прямоугольных сечений только с растянутой арматурой высоту сжатой зоны определяют по формуле

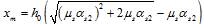
, (7.41)

где

.

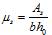
Для прямоугольных сечений с растянутой и сжатой арматурой высоту сжатой зоны определяют по формуле

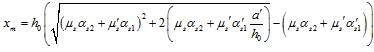
, (7.42)

где

.

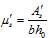
Для тавровых (с полкой в сжатой зоне) и двутавровых сечений высоту сжатой зоны определяют по формуле

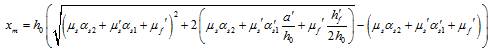
, (7.43)

где

.

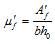
A‘_f — площадь сечения свесов сжатой полки.

Для внецентренно сжатых и внецентренно растянутых элементов положение нейтральной оси (высоту сжатой зоны) определяют из уравнения

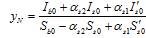
, (7.44)

где y_N — расстояние от нейтральной оси до точки приложения продольной силы N, отстоящей от центра тяжести полного сечения (без учета трещин) на расстоянии ;

I_b0, I_s0, I‘_s0, S_b0, S_s0, S‘_s0 — моменты инерции и статические моменты соответственно сжатой зоны бетона, растянутой и сжатой арматуры относительно нейтральной оси.

Допускается для элементов прямоугольного сечения высоту сжатой зоны при действии изгибающих моментов M продольной силы N определять по формуле

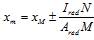
, (7.45)

где х_M — высота сжатой зоны изгибаемого элемента, определяемая по формулам (7.40)—(7.43);

I_red, A_red — момент инерции и площадь приведенного поперечного сечения, определяемые для полного сечения (без учета трещин).

Значения геометрических характеристик сечения элемента определяют по общим правилам расчета сечения упругих элементов.

В формуле (7.45) знак «плюс» принимают при сжимающей, а знак «минус» — при растягивающей продольной силе.

7.3.13 Жесткость изгибаемых железобетонных элементов допускается определять по формуле

D = E_s,red A_s z (h₀ — x_m), (7.46)

где z — расстояние от центра тяжести растянутой арматуры до точки приложения равнодействующей усилий в сжатой зоне.

Для элементов прямоугольного сечения при отсутствии (или без учета) сжатой арматуры значение z определяют по формуле

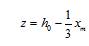
. (7.47)

Для элементов прямоугольного, таврового (с полкой в сжатой зоне) и двутаврового поперечных сечений значение z допускается принимать равным 0,8 h₀.

7.3.14 Значения коэффициентов приведения арматуры к бетону принимают равными:

для сжатой арматуры

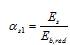
; (7.48)

для растянутой арматуры

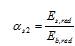
; (7.49)

где Е_b,red — приведенный модуль деформации сжатого бетона, определяемый по формуле (5.9), при непродолжительном и продолжительном действии нагрузки;

E_s,red — приведенный модуль деформации растянутой арматуры, определяемый с учетом влияния работы растянутого бетона между трещинами по формуле

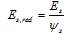
. (7.50)

Значения коэффициента y_s определяют по формуле (7.22).

Допускается принимать y_s = 1 и следовательно a_s2 = a_s1. При этом, если условие (7.24) не удовлетворяется, расчет производят с учетом коэффициента y_s по формуле (7.23).

7.3.15 Прогибы железобетонных элементов можно определять по общим правилам строительной механики с использованием вместо кривизны непосредственно изгибных жесткостных характеристик D путем замены упругих изгибных характеристик EJ в расчетных зависимостях на указанные характеристики D, вычисляемые по формулам, приведенным в 7.3.9 и 7.3.13.

При совместном действии кратковременной и длительной нагрузок полный прогиб элементов без трещин и с трещинами в растянутой зоне определяют путем суммирования прогибов от соответствующих нагрузок по аналогии с суммированием кривизны согласно 7.3.8, принимая жесткостные характеристики D в зависимости от указанной в этом пункте принятой продолжительности действия рассматриваемой нагрузки.

Допускается при определении жесткостных характеристик D элементов с трещинами в растянутой зоне принимать коэффициент y_s = 1. В этом случае при совместном действии кратковременной и длительной нагрузок полный прогиб элементов с трещинами определяют путем суммирования прогибов от непродолжительного действия кратковременной нагрузки и от продолжительного действия длительной нагрузки с учетом соответствующих значений жесткостных характеристик D, т.е. подобно тому, как это принято для элементов без трещин.

Определение кривизны железобетонных элементов на основе нелинейной деформационной модели

7.3.16 Полную кривизну железобетонных элементов на участках без трещин в растянутой зоне сечения определяют по формуле (7.28), а на участках с трещинами в растянутой зоне сечения — по формуле (7.29).

Значения кривизны, входящие в формулы (7.28) и (7.29), определяют из решения системы уравнений (6.36)—(6.40). При этом для элементов с нормальными трещинами в растянутой зоне напряжение в арматуре, пересекающей трещины, определяют по формуле

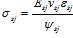
, (7.51)

где

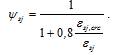
. (7.52)

Здесь e_sj,crc — относительная деформация растянутой арматуры в сечении с трещиной сразу после образования нормальных трещин;

e_sj — усредненная относительная деформация растянутой арматуры, пересекающей трещины, в рассматриваемой стадии расчета.

При определении кривизны от непродолжительного действия нагрузки в расчете используют диаграммы кратковременного деформирования сжатого и растянутого бетона, а при определении кривизны от продолжительного действия нагрузки — диаграммы длительного деформирования бетона с расчетными характеристиками для предельных состояний второй группы.

Для частных случаев действия внешней нагрузки (изгиб в двух плоскостях, изгиб в плоскости оси симметрии поперечного сечения элемента и т.п.) кривизны, входящие в формулы (7.28) и (7.29), определяют из решения систем уравнений, указанных в 6.2.27—6.2.29.

8 КОНСТРУКТИВНЫЕ ТРЕБОВАНИЯ

8.1 ОБЩИЕ ПОЛОЖЕНИЯ

8.1.1 Для обеспечения несущей способности, пригодности к нормальной эксплуатации и долговечности бетонных и железобетонных конструкций помимо требований, определяемых расчетом, следует выполнять конструктивные требования:

— по геометрическим размерам элементов конструкций;

— по армированию (содержанию и расположению арматуры, толщине защитного слоя бетона, анкеровке и соединениям арматуры);

— по защите конструкций от неблагоприятного влияния воздействий среды.

8.2 ГЕОМЕТРИЧЕСКИЕ РАЗМЕРЫ КОНСТРУКЦИЙ

8.2.1 Минимальные геометрические размеры сечений конструкций следует назначать такими, чтобы обеспечивать:

— возможность надлежащего размещения арматуры (расстояния между стержнями, защитный слой бетона и т.д.), ее анкеровки и совместной работы с бетоном;

— достаточную жесткость конструкций;

— необходимую огнестойкость, водонепроницаемость конструкций, тепло- и звукоизоляцию, коррозионную стойкость, радиационную защиту и т.п.;

— возможность качественного изготовления при бетонировании конструкций,

8.2.2 Размеры сечений внецентренно сжатых элементов для обеспечения их жесткости рекомендуется принимать такими, чтобы их гибкость в любом направлении не превышала:

200 — для железобетонных элементов;

120 — для колонн, являющихся элементами зданий;

90 — для бетонных элементов.

8.2.3 В конструкциях зданий и сооружений следует предусматривать их разрезку постоянными и временными температурно-усадочными швами, расстояния между которыми назначают в зависимости от климатических условий, конструктивных особенностей сооружения, последовательности производства работ и т.п.

При неравномерной осадке фундаментов следует предусматривать разделение конструкций осадочными швами.

8.3 АРМИРОВАНИЕ

Защитный слой бетона

8.3.1 Арматура, расположенная внутри сечения конструкции, должна иметь защитный слой бетона (расстояние от поверхности арматуры до соответствующей грани конструкций), чтобы обеспечивать:

— совместную работу арматуры с бетоном;

— анкеровку арматуры в бетоне и возможность устройства стыков арматурных элементов;

— сохранность арматуры от воздействий окружающей среды (в том числе при наличии агрессивных воздействий);

— огнестойкость и огнесохранность.

8.3.2 Толщину защитного слоя бетона назначают исходя из требований 8.3.1 с учетом типа конструкций, роли арматуры в конструкциях (продольная рабочая, поперечная, распределительная, конструктивная арматура), условий окружающей среды и диаметра арматуры.

Минимальные значения толщины слоя бетона рабочей арматуры следует принимать по таблице 8.1.

Таблица 8.1

Условия эксплуатации конструкций зданий	Толщина защитного слоя бетона, мм, не менее
1. В закрытых помещениях при нормальной и пониженной влажности	20
2. В закрытых помещениях при повышенной влажности (при отсутствии дополнительных защитных мероприятий)	25
3. На открытом воздухе (при отсутствии дополнительных защитных мероприятий)	30
4. В грунте (при отсутствии дополнительных защитных мероприятий), в фундаментах при наличии бетонной подготовки	40

Для сборных элементов минимальные значения толщины защитного слоя бетона рабочей арматуры, указанные в таблице 8.1, уменьшают на 5 мм.

Для конструктивной арматуры минимальные значения толщины защитного слоя бетона принимают на 5 мм меньше по сравнению с требуемыми для рабочей арматуры.

Во всех случаях толщину защитного слоя бетона следует также принимать не менее диаметра стержня арматуры.

Минимальные расстояния между стержнями арматуры

8.3.3 Минимальные расстояния в свету между стержнями арматуры следует принимать такими, чтобы обеспечить совместную работу арматуры с бетоном и качественное изготовление конструкций, связанное с укладкой и уплотнением бетонной смеси, но не менее наибольшего диаметра стержня, а также не менее:

25 мм — при горизонтальном или наклонном положении стержней при бетонировании для нижней арматуры, расположенной в один или два ряда;

30 мм — то же, для верхней арматуры;

50 мм — то же, при расположении нижней арматуры более чем в два ряда (кроме стержней двух нижних рядов), а также при вертикальном положении стержней при бетонировании.

При стесненных условиях допускается располагать стержни группами — пучками (без зазора между ними). При этом расстояния в свету между пучками должны быть также не менее приведенного диаметра стержня, эквивалентного по площади сечения пучка арматуры, принимаемого равным:

,

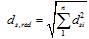
где d_si — диаметр одного стержня в пучке;

n — число стержней в пучке.

Продольное армирование

8.3.4 В железобетонных элементах площадь сечения продольной растянутой арматуры, а также сжатой, если она требуется по расчету, в процентах площади сечения бетона, равной произведению ширины прямоугольного сечения либо ширины ребра таврового (двутаврового) сечения на рабочую высоту сечения, следует принимать не менее:

0,1 % — в изгибаемых, внецентренно растянутых элементах и внецентренно сжатых элементах при гибкости (для прямоугольных сечений );

0,25 % — во внецентренно сжатых элементах при гибкости (для прямоугольных сечений );

для промежуточных значений гибкости элементов значение m_s определяют по интерполяции.

В элементах с продольной арматурой, расположенной равномерно по контуру сечения, а также в центрально-растянутых элементах минимальную площадь сечения всей продольной арматуры следует принимать вдвое больше указанных выше значений и относить их к полной площади сечения бетона.

8.3.5 В бетонных конструкциях следует предусматривать конструктивное армирование:

— в местах резкого изменения размеров сечения элементов;

— в бетонных стенах под и над проемами;

— во внецентренно сжатых элементах, рассчитываемых по прочности без учета работы растянутого бетона, у граней, где возникают растягивающие напряжения; при этом коэффициент армирования m_s принимают не менее 0,025 %.

8.3.6 В железобетонных линейных конструкциях и плитах наибольшие расстояния между осями стержней продольной арматуры, обеспечивающие эффективное вовлечение в работу бетона, равномерное распределение напряжений и деформаций, а также ограничение ширины раскрытия трещин между стержнями арматуры, должны быть не более:

в железобетонных балках и плитах:

200 мм — при высоте поперечного сечения h £ 150 мм;

1,5h и 400 мм — при высоте поперечного сечения h > 150 мм;

в железобетонных колоннах:

400 мм — в направлении, перпендикулярном плоскости изгиба;

500 мм — в направлении плоскости изгиба.

В железобетонных стенах расстояния между стержнями вертикальной арматуры принимают не более 2t и 400 мм (t — толщина стены), а горизонтальной — не более 400 мм.

8.3.7 В балках и ребрах шириной более 150 мм число продольных рабочих растянутых стержней в поперечном сечении должно быть не менее двух. При ширине элемента 150 мм и менее допускается устанавливать в поперечном сечении один продольный стержень.

8.3.8 В балках до опоры следует доводить стержни продольной рабочей арматуры с площадью сечения не менее ¹/₂ площади сечения стержней в пролете и не менее двух стержней.

В плитах до опоры следует доводить стержни продольной рабочей арматуры на 1 м ширины плиты с площадью сечения не менее ¹/₃ площади сечения стержней на 1 м ширины плиты в пролете.

Поперечное армирование

8.3.9 Поперечную арматуру следует устанавливать исходя из расчета на восприятие усилий, а также с целью ограничения развития трещин, удержания продольных стержней в проектном положении и закрепления их от бокового выпучивания в любом направлении.

Поперечную арматуру устанавливают у всех поверхностей железобетонных элементов, вблизи которых ставится продольная арматура.

8.3.10 Диаметр поперечной арматуры (хомутов) в вязаных каркасах внецентренно сжатых элементов принимают не менее 0,25 наибольшего диаметра продольной арматуры и не менее 6 мм.

Диаметр поперечной арматуры в вязаных каркасах изгибаемых элементов принимают не менее 6 мм.

В сварных каркасах диаметр поперечной арматуры принимают не менее диаметра, устанавливаемого из условия сварки с наибольшим диаметром продольной арматуры.

8.3.11 В железобетонных элементах, в которых поперечная сила по расчету не может быть воспринята только бетоном, следует предусматривать установку поперечной арматуры с шагом не более 0,5 h₀ и не более 300 мм.

В сплошных плитах, а также в часторебристых плитах высотой менее 300 мм и в балках (ребрах) высотой менее 150 мм на участке элемента, где поперечная сила по расчету воспринимается только бетоном, поперечную арматуру можно не устанавливать.

В балках и ребрах высотой 150 мм и более, а также в часторебристых плитах высотой 300 мм и более, на участках элемента, где поперечная сила по расчету воспринимается только бетоном, следует предусматривать установку поперечной арматуры с шагом не более 0,75 h₀и не более 500 мм.

8.3.12 Во внецентренно сжатых линейных элементах, а также в изгибаемых элементах при наличии необходимой по расчету сжатой продольной арматуры с целью предотвращения выпучивания продольной арматуры следует устанавливать поперечную арматуру с шагом не более 15d и не более 500 мм (d — диаметр сжатой продольной арматуры).

Если площадь сечения сжатой продольной арматуры, устанавливаемой у одной из граней элемента, более 1,5 %, поперечную арматуру следует устанавливать с шагом не более 10d и не более 300 мм.

8.3.13 Конструкция хомутов (поперечных стержней) во внецентренно сжатых линейных элементах должна быть такой, чтобы продольные стержни (по крайней мере через один) располагались в местах перегибов, а эти перегибы — на расстоянии не более 400 мм по ширине грани. При ширине грани не более 400 мм и числе продольных стержней у этой грани не более четырех допускается охват всех продольных стержней одним хомутом.

8.3.14 В элементах, на которые действуют крутящие моменты, поперечная арматура (хомуты) должна образовывать замкнутый контур.

8.3.15 Поперечную арматуру в плитах в зоне продавливания в направлении, перпендикулярном сторонам расчетного контура, устанавливают с шагом не более ¹/₃h₀ и не более 300 мм. Стержни, ближайшие к контуру грузовой площади, располагают не ближеh₀/3 и не далее h₀/2 от этого контура. При этом ширина зоны постановки поперечной арматуры (от контура грузовой площади) должна быть не менее ¹/₅h₀.

Расстояния между стержнями поперечной арматуры в направлении, параллельном сторонам расчетного контура, принимают не более ¹/₄ длины соответствующей стороны расчетного контура.

8.3.16 Расчетную поперечную арматуру в виде сеток косвенного армирования при местном сжатии (смятии) располагают в пределах расчетной площади A_b,max (6.2.43). При расположении грузовой площади у края элемента сетки косвенного армирования располагают по площади с размерами в каждом направлении не менее суммы двух взаимно перпендикулярных сторон грузовой площади (рисунок 6.11).

По глубине сетки располагают:

— при толщине элемента более удвоенного большего размера грузовой площади — в пределах удвоенного размера грузовой площади;

— при толщине элемента менее удвоенного большего размера грузовой площади — в пределах толщины элемента.

8.3.17 Поперечная арматура, предусмотренная для восприятия поперечных сил и крутящих моментов, а также учитываемая при расчете на продавливание, должна иметь надежную анкеровку по концам путем приварки или охвата продольной арматуры, обеспечивающую равнопрочность соединений и поперечной арматуры.

Анкеровка арматуры

8.3.18 Анкеровку арматуры осуществляют одним из следующих способов или их сочетанием:

— в виде прямого окончания стержня (прямая анкеровка);

— с загибом на конце стержня в виде крюка, отгиба (лапки) или петли;

— с приваркой или установкой поперечных стержней;

— с применением специальных анкерных устройств на конце стержня.

8.3.19 Прямую анкеровку и анкеровку с лапками допускается применять только для арматуры периодического профиля. Для растянутых гладких стержней следует предусматривать крюки, петли, приваренные поперечные стержни или специальные анкерные устройства.

Лапки, крюки и петли не рекомендуется применять для анкеровки сжатой арматуры, за исключением гладкой арматуры, которая может подвергаться растяжению при некоторых возможных сочетаниях нагрузки.

8.3.20 При расчете длины анкеровки арматуры следует учитывать способ анкеровки, класс арматуры и ее профиль, диаметр арматуры, прочность бетона и его напряженное состояние в зоне анкеровки, конструктивное решение элемента в зоне анкеровки (наличие поперечной арматуры, положение стержней в сечении элемента и др.).

8.3.21 Базовую (основную) длину анкеровки, необходимую для передачи усилия в арматуре с полным расчетным значением сопротивления R_s на бетон, определяют по формуле

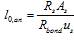
, (8.1)

где A_s и u_s — соответственно площадь поперечного сечения анкеруемого стержня арматуры и периметр его сечения, определяемые по номинальному диаметру стержня;

R_bond — расчетное сопротивление сцепления арматуры с бетоном, принимаемое равномерно распределенным по длине анкеровки и определяемое по формуле

R_bond = h₁ h₂R_bt, (8-2)

здесь R_bt — расчетное сопротивление бетона осевому растяжению;

h₁ — коэффициент, учитывающий влияние вида поверхности арматуры, принимаемый равным:

1,5 — для гладкой арматуры;

2 — для холоднодеформированной арматуры периодического профиля;

2,5 — для горячекатаной и термомеханически обработанной арматуры периодического профиля;

h₂ — коэффициент, учитывающий влияние размера диаметра арматуры, принимаемый равным:

1,0 — при диаметре арматуры d_s £ 32 мм;

0,9 — при диаметре арматуры 36 и 40 мм.

8.3.22 Требуемую расчетную длину анкеровки арматуры с учетом конструктивного решения элемента в зоне анкеровки определяют по формуле

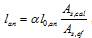
, (8.3)

где l_0,an — базовая длина анкеровки, определяемая по формуле (8.1);

A_s,cal, A_s,ef — площади поперечного сечения арматуры, соответственно требуемая по расчету и фактически установленная;

a — коэффициент, учитывающий влияние на длину анкеровки напряженного состояния бетона и арматуры и конструктивного решения элемента в зоне анкеровки.

При анкеровке стержней периодического профиля с прямыми концами (прямая анкеровка) или гладкой арматуры с крюками или петлями без дополнительных анкерующих устройств для растянутых стержней принимают a = 1,0, а для сжатых — a = 0,75.

Допускается уменьшать длину анкеровки в зависимости от количества и диаметра поперечной арматуры, вида анкерующих устройств (приварка поперечной арматуры, загиб концов стержней периодического профиля) и величины поперечного обжатия бетона в зоне анкеровки (например, от опорной реакции), но не более чем на 30 %.

В любом случае фактическую длину анкеровки принимают не менее 0,3l_0,an, а также не менее 15 d_s и 200 мм.

8.3.23 Усилие, воспринимаемое анкеруемым стержнем арматуры N_s, определяют по формуле

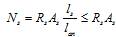
, (8.4)

где l_an — длина анкеровки, определяемая согласно 8.3.22, принимая отношение

;

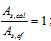
l_s — расстояние от конца анкеруемого стержня до рассматриваемого поперечного сечения элемента.

8.3.24 На крайних свободных опорах элементов длина запуска растянутых стержней за внутреннюю грань свободной опоры при выполнении условия Q £ Q_b1 (6.2.32—6.2.35) должна составлять не менее 5 d_s. Если указанное условие не соблюдается, длину запуска арматуры за грань опоры определяют согласно 8.3.22.

8.3.25 При устройстве на концах стержней специальных анкеров в виде пластин, шайб, гаек, уголков, высаженных головок и т.п. площадь контакта анкера с бетоном должна удовлетворять условию прочности бетона на смятие. Кроме того, при проектировании привариваемых анкерных деталей следует учитывать характеристики металла по свариваемости, а также способы и условия сварки.

Соединения арматуры

8.3.26 Для соединения арматуры принимают один из следующих типов стыков:

а) стыки внахлестку без сварки:

— с прямыми концами стержней периодического профиля;

— с прямыми концами стержней с приваркой или установкой на длине нахлестки поперечных стержней;

— с загибами на концах (крюки, лапки, петли); при этом для гладких стержней применяют только крюки и петли;

б) сварные и механические стыковые соединения:

— со сваркой арматуры;

— с применением специальных механических устройств (стыки с опрессованными муфтами, резьбовыми муфтами и др.).

8.3.27 Стыки арматуры внахлестку (без сварки) применяют при стыковании стержней с диаметром рабочей арматуры не более 40 мм.

На соединения арматуры внахлестку распространяются указания 8.3.19.

Стыки растянутой или сжатой арматуры должны иметь длину перепуска (нахлестки) не менее значения длины l_l определяемого по формуле

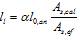
, (8.5)

где l_0,an — базовая длина анкеровки, определяемая по формуле (8.1);

A_s,cal, A_s,ef — по 8.3.22;

a — коэффициент, учитывающий влияние напряженного состояния арматуры, конструктивного решения элемента в зоне соединения стержней, количество стыкуемой арматуры в одном сечении по отношению к общему количеству арматуры в этом сечении, расстояния между стыкуемыми стержнями.

При соединении арматуры периодического профиля с прямыми концами, а также гладких стержней с крюками или петлями без дополнительных анкерующих устройств коэффициент a для растянутой арматуры принимают равным 1,2, а для сжатой арматуры — 0,9. При этом должны быть соблюдены следующие условия:

— относительное количество стыкуемой в одном расчетном сечении элемента рабочей растянутой арматуры периодического профиля должно быть не более 50 %, гладкой арматуры (с крюками или петлями) — не более 25 %;

— усилие, воспринимаемое всей поперечной арматурой, поставленной в пределах стыка, должно быть не менее половины усилия, воспринимаемого стыкуемой в одном расчетном сечении элемента растянутой рабочей арматурой;

— расстояние между стыкуемыми рабочими стержнями арматуры не должно превышать 4d_s;

— расстояние между соседними стыками внахлестку (по ширине железобетонного элемента) должно быть не менее 2 d_s и не менее 30 мм.

В качестве одного расчетного сечения элемента, рассматриваемого для определения относительного количества стыкуемой арматуры в одном сечении, принимают участок элемента вдоль стыкуемой арматуры длиной 1,3 l_l. Считается, что стыки арматуры расположены в одном расчетном сечении, если центры этих стыков находятся в пределах длины этого участка.

Допускается увеличивать относительное количество стыкуемой в одном расчетном сечении элемента рабочей растянутой арматуры до 100 %, принимая значение коэффициента a равным 2,0. При относительном количестве стыкуемой в одном расчетном сечении арматуры периодического профиля более 50 % и гладкой арматуры более 25 % значения коэффициента a определяют по линейной интерполяции.

При наличии дополнительных анкерующих устройств на концах стыкуемых стержней (приварка поперечной арматуры, загиб концов стыкуемых стержней периодического профиля и др.) длина перепуска стыкуемых стержней может быть уменьшена, но не более чем на 30 %.

В любом случае фактическая длина перепуска должна быть не менее 0,4al_0,an, не менее 20 d_sи не менее 250 мм.

8.3.28 При соединении арматуры с использованием сварки выбор типов сварного соединения и способов сварки производят с учетом условий эксплуатации конструкции, свариваемости стали и требований по технологии изготовления в соответствии с действующими нормативными документами (ГОСТ 14098).

8.3.29 При использовании для стыков арматуры механических устройств в виде муфт (муфты на резьбе, опрессованные муфты и т.д.) несущая способность муфтового соединения должна быть такой же, что и стыкуемых стержней (соответственно при растяжении или сжатии). Концы стыкуемых стержней следует заводить на требуемую длину в муфту, определяемую расчетом или опытным путем.

При использовании муфт на резьбе должна быть обеспечена требуемая затяжка муфт для ликвидации люфта в резьбе.

Гнутые стержни

8.3.30 При применении гнутой арматуры (отгибы, загибы концов стержней) минимальный диаметр загиба отдельного стержня должен быть таким, чтобы избежать разрушения или раскалывания бетона внутри загиба арматурного стержня и его разрушения в месте загиба.

Минимальный диаметр оправки d_on для арматуры принимают в зависимости от диаметра стержня d_s не менее:

для гладких стержней:

d_on = 2,5 d_s при d_s < 20 мм;

d_on = 4 d_s при d_s ³ 20 мм;

для стержней периодического профиля:

d_on = 5 d_s при d_s < 20 мм;

d_on = 8 d_s при d_s ³ 20 мм.

ПРИЛОЖЕНИЕ А

(Справочное)

ОСНОВНЫЕ БУКВЕННЫЕ ОБОЗНАЧЕНИЯ

Усилия от внешних нагрузок и воздействий в поперечном сечении элемента

М — изгибающий момент;

N — продольная сила;

Q — поперечная сила;

Т — крутящий момент.

Характеристики материалов

Rb,n	—	нормативное сопротивление бетона осевому сжатию;
Rb, Rb,ser	—	расчетные сопротивления бетона осевому сжатию для предельных состояний соответственно первой и второй групп;
Rbt,n	—	нормативное сопротивление бетона осевому растяжению;
Rbt, Rbt,ser	—	расчетные сопротивления бетона осевому растяжению для предельных состояний соответственно первой и второй групп;
Rb,loc	—	расчетное сопротивление бетона смятию;
Rbond	—	расчетное сопротивление сцепления арматуры с бетоном;
Rs, Rs,ser	—	расчетные сопротивления арматуры растяжению для предельных состояний соответственно первой и второй групп;
Rsw	—	расчетное сопротивление поперечной арматуры растяжению;
Rsc	—	расчетное сопротивление арматуры сжатию для предельных состояний первой группы;
Eb	—	начальный модуль упругости бетона при сжатии и растяжении;
Es	—	модуль упругости арматуры;
eb0, ebt0	—	предельные относительные деформации бетона соответственно при равномерном осевом сжатии и осевом растяжении;
es0	—	относительные деформации арматуры при напряжении, равном Rs;
jb,cr	—	коэффициент ползучести бетона.

Характеристики положения продольной арматуры в поперечном сечении элемента

S	—	обозначение продольной арматуры:при наличии сжатой и растянутой от действия внешней нагрузки зон сечения — расположенной в растянутой зоне;при полностью сжатом от действия внешней нагрузки сечении — расположенной у менее сжатой грани сечения; при полностью растянутом от действия внешней нагрузки сечении: для внецентренно растянутых элементов — расположенной у более растянутой грани сечения; для центрально-растянутых элементов — всей в поперечном сечении элемента;
S‘	—	обозначение продольной арматуры:при наличии сжатой и растянутой от действия внешней нагрузки зон сечения — расположенной в сжатой зоне;при полностью сжатом от действия внешней нагрузки сечении — расположенной у более сжатой грани сечения; при полностью растянутом от действия внешней нагрузки сечении внецентренно растянутых элементов — расположенной у менее растянутой грани сечения.

Геометрические характеристики

b	—	ширина прямоугольного сечения; ширина ребра таврового и двутаврового сечений;
bf, b’f	—	ширина полки таврового и двутаврового сечений соответственно в растянутой и сжатой зонах;
h	—	высота прямоугольного, таврового и двутаврового сечений;
hf, h’f	—	высота полки таврового и двутаврового сечений соответственно в растянутой и сжатой зонах;
a, a’	—	расстояние от равнодействующей усилий в арматуре соответственно S и S‘ до ближайшей грани сечения;
h0, h’0	—	рабочая высота сечения, равная соответственно h—а и h—а’;
x	—	высота сжатой зоны бетона;
x	—	относительная высота сжатой зоны бетона, равная ;
sw	—	расстояние между хомутами, измеренное по длине элемента;
e0	—	эксцентриситет продольной силы N относительно центра тяжести приведенного сечения, определяемый с учетом указаний 4.2.6;
e, e’	—	расстояния от точки приложения продольной силы N до равнодействующей усилий в арматуре соответственно S и S‘;
l	—	пролет элемента;
l0	—	расчетная длина элемента, подвергающегося действию сжимающей продольной силы;
i	—	радиус инерции поперечного сечения элемента относительно центра тяжести сечения;
ds, dsw	—	номинальный диаметр стержней соответственно продольной и поперечной арматуры;
As, A’s	—	площади сечения арматуры соответственно S и S‘;
Asw	—	площадь сечения хомутов, расположенных в одной нормальной к продольной оси элемента плоскости, пересекающей наклонное сечение;
ms	—	коэффициент армирования, определяемый как отношение площади сечения арматуры S к площади поперечного сечения элемента bh0 без учета свесов сжатых и растянутых полок;
A	—	площадь всего бетона в поперечном сечении;
Ab	—	площадь сечения бетона сжатой зоны;
Abt	—	площадь сечения бетона растянутой зоны;
Ared	—	площадь приведенного сечения элемента;
Aloc	—	площадь смятия бетона;
I	—	момент инерции сечения всего бетона относительно центра тяжести сечения элемента;
Ired	—	момент инерции приведенного сечения элемента относительно его центра тяжести;
W	—	момент сопротивления сечения элемента для крайнего растянутого волокна.

Ключевые слова: основные расчетные требования к бетонным и железобетонным конструкциям, материалы для бетонных и железобетонных конструкций, конструктивные требования к бетонным и железобетонным конструкциям, расчет бетонных и железобетонных элементов по прочности

СОДЕРЖАНИЕ

Введение

1 Область применения

2 Нормативные ссылки

3 Термины и определения

4 Общие указания

4.1 Основные положения

4.2 Основные расчетные требования

5 Материалы для бетонных и железобетонных конструкций

5.1 Бетон

5.2 Арматура

6 Расчет элементов бетонных и железобетонных конструкций по предельным состояниям первой группы

6.1 Расчет бетонных элементов по прочности

6.2 Расчет железобетонных элементов по прочности

7 Расчет элементов железобетонных конструкций по предельным состояниям второй группы

7.1 Общие положения

7.2 Расчет железобетонных элементов по раскрытию трещин

7.3 Расчет элементов железобетонных конструкций по деформациям

8 Конструктивные требования

8.1 Общие положения

8.2 Геометрические размеры конструкций

8.3 Армирование