Способ вычисления квадрата любого двухзначного числа без умножения столбиком

Когда требуется найти квадрат какого-либо двузначного числа, это обычно не представляет большой сложности – достаточно умножить число само на себя, используя столбиковое умножение. Однако, что делать, если необходимо вычислить множество квадратов? Например, найти квадраты всех чисел от 70 до 80? В данном случае повторять столбиковое умножение 11 раз может оказаться не слишком удобным.

В общем, показываю алгоритм, по которому все это находится буквально за секунды.

1. Нужно найти квадраты круглых чисел. В нашем случае квадраты 70 и 80 соответственно равны 4900 и 6400 — это легко. Плюс желательно вспомнить квадрат 75. У меня есть отдельная статья о том, как возводить в квадрат числа, заканчивающиеся на 5, но если коротко, то в конце надо написать 25, а в начале записать произведение 7•(7+1)=56. То есть 75²=5625. На картинке ниже изобразил схематично.

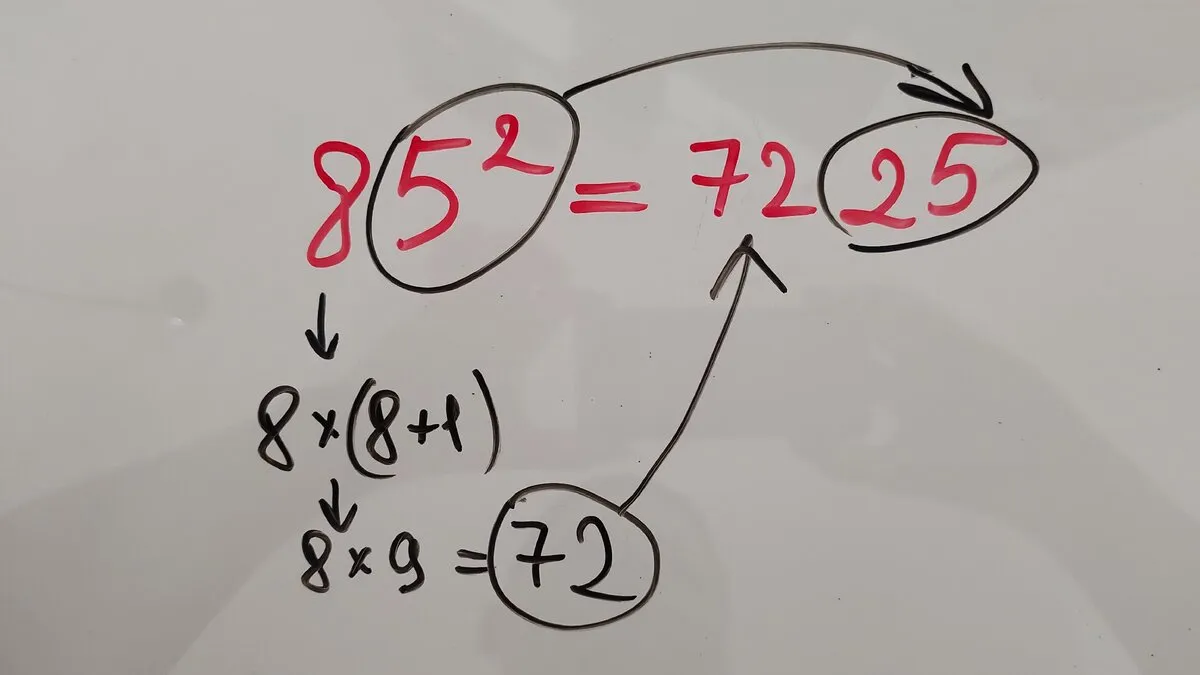
2. Дальше действуем по алгоритму. Числа 71 и 72 находятся ближе к 70, 73, 74, 76 и 77 ближе к 75, а 78 и 79 — к 80. На это мы будем опираться при вычислениях. Сейчас всё поймете. Чтобы считать быстрее, рекомендую прочитать мою статью о способах быстрого сложения и вычитания больших числе в уме.

71²=70²+70+71=4900+70+71=5041.

По такому же алгоритму считаем 76, но опираться будет не на 70, а на 75:

76²=75²+75+76=5625+75+76=5776.

С 74 и 79 почти точно так же, только мы не складываем, а отнимаем, так эти числа стоят слева от опорных 75 и 80.

74²=75²-75-74=5625-75-74=5550-74=5476.

79²=80²-80-79=6900-80-79=6320-79=6241.

3. Числа, которые стоят через одно от опорного, считаются чуть-чуть по-другому.

72²=70²+4•71=4900+284=5184

77²=75²+4•76=5625+304=5929

В числах, которые левее опорных, делаем вычитание вместо сложения:

73²=75²-4•74=5625-280-16=5329

78²=80²-4•79=640-320+4=6084.

На первый взгляд кажется сложно и громоздко, но стоит один раз понять, освоить и попробовать, как все сразу становится на свои места, и вы буквально за секунды сможете находить квадраты двухзначных чисел, немного потренировавшись и запомнив алгоритм.

Для простоты, постарался записать для вас алгоритм действий на одном листе. Сохраните картинку или лайкните этот пост. Можно будет поражать всех своим умением быстро считать в уме.

Напоминаю, тем кто ещё не подписался, что у меня появился одноименный канал на Ютубе, где я делюсь решениями интересных задач и всякими математическими и физическими хитростями.

Ещё интересно: Два простых способа быстрого сложения и вычитания в уме

90% европейских выпускников не смогли решить задачу, которую решили российские восьмиклассники

Простой и очень быстрый способ возведения в квадрат чисел, оканчивающихся на 5

Как найти площадь сложной фигуры по клеткам?

Чтобы найти площадь сложной фигуры по клеткам, вам нужно разбить эту фигуру на более простые фигуры, такие как прямоугольники, квадраты, треугольники и т.д., а затем найти площадь каждой из этих более простых фигур и сложить их вместе. Вот несколько шагов, которые помогут вам выполнить это:

1. Нарисуйте фигуру на клетчатой бумаге, чтобы она была максимально точной и правильной.

2. Разбейте фигуру на более простые геометрические фигуры, такие как квадраты, прямоугольники, треугольники и т.д. Обычно удобно выбирать такие фигуры, чтобы они были прямоугольными.

3. Измерьте длину и ширину каждой из более простых фигур в клетках на бумаге, и используйте эти измерения для вычисления площади каждой фигуры. Например, площадь прямоугольника можно вычислить, умножив его длину на ширину.

4. Сложите площади каждой из более простых фигур, чтобы найти общую площадь исходной сложной фигуры.

Обратите внимание, что если в сложной фигуре есть отверстия, например, круги, то их площадь также необходимо вычесть из общей площади.

Видео. Умножение в столбик. Как правильно умножать в столбик? Как объяснить умножение в столбик?