Расчет площади квадрата: формула для нахождения площади квадрата со стороной 3 метра

Формула нахождения площади квадрата

Квадрат —

Это геометрическая фигура, которая представляет собой частный случай прямоугольника, что обусловливает сходство некоторых алгоритмов. Метод вычисления всегда определяется исходными данными. Если у вас есть задача «найди площадь квадрата со сторонами 3 метра каждая», то следующий текст будет содержать подробное решение…

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Если известна длина стороны

Умножаем ее на то же число или возводим в квадрат.

S = a × a = a2, где S — площадь, a — сторона.

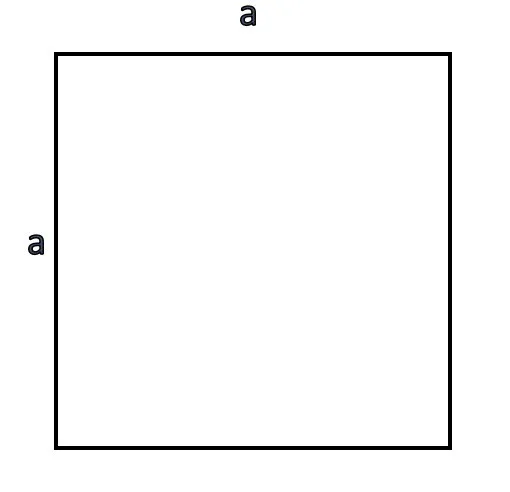
Эту формулу проходят в 3 классе. Остальные формулы третьеклассникам знать пока не нужно, но они пригодятся ученикам 8 класса.

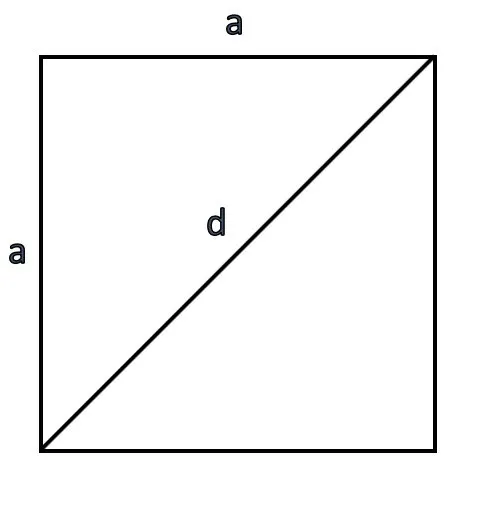
Если нам дана диагональ

Возводим ее в квадрат и делим на два.

S = d2 : 2, где d — диагональ.

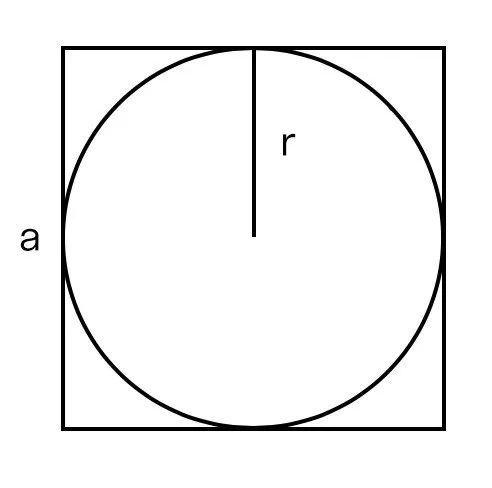
Если известен радиус вписанной окружности

Умножаем его квадрат на четыре.

S = 4 × r2, где r — это радиус вписанной окружности.

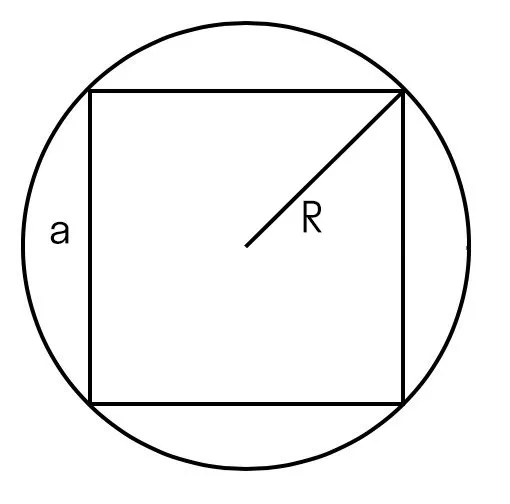
Если у нас есть радиус описанной окружности

Возведем его в квадрат и умножим на два.

S = 2 × R2, где R — это радиус описанной окружности.

Если есть периметр

Мы должны возвести его в квадрат и разделить на 16.

S = Р2 : 16, где Р — это периметр.

Периметр любого четырехугольника равен сумме длин всех его сторон.

Важно!

Задачку не решить, если длина и ширина даны в разных единицах. Для правильного решения переведите все данные к одной единице измерения, и все получится.

Популярные единицы измерения площади:

• квадратный миллиметр (мм2);
• квадратный сантиметр (см2);
• квадратный дециметр (дм2);
• квадратный метр (м2);
• квадратный километр (км2);
• гектар (га).

S квадрата. Решение задач

Мы разобрали пять формул для вычисления площади квадрата. А теперь давайте потренируемся!

Задание 1. Как найти площадь квадрата, диагональ которого равна 90 мм.

Как решаем:

1. Воспользуемся формулой: S = d2 : 2.

2. Подставим в формулу значение диагонали: S = 902 : 2 = 4050 мм2.

Ответ: 4050 мм2.

Задание 2. Окружность вписана в квадрат. Найдите площадь квадрата, если радиус окружности равен 24 см.

Как решаем:

1. Если окружность вписана в квадрат, то сторона квадрата равна диаметру:
   a = d

2. Диаметр окружности равен двум радиусам:
   d = 2r

3. Получается, что сторона равна двум радиусам:
   a = 2r

4. Используем формулу нахождения площади квадрата через сторону:
   S = a2

5. Так как из пункта 3 мы получили, что сторона равна двум радиусам, то формула площади квадрата примет вид:
   S = (2r)2
   S = 4r2

6. Теперь подставим значение радиуса в формулу площади:
   S = 4 × 242 = 2304 см2

Ответ: 2304 см2.

Как найти длину стороны квадрата через площадь?

Длина стороны квадрата может быть найдена через его площадь, используя формулу: сторона = sqrt(площадь), где sqrt — квадратный корень.

Например, если площадь квадрата равна 16 кв. единиц, то длина стороны равна sqrt(16) = 4 единицы.