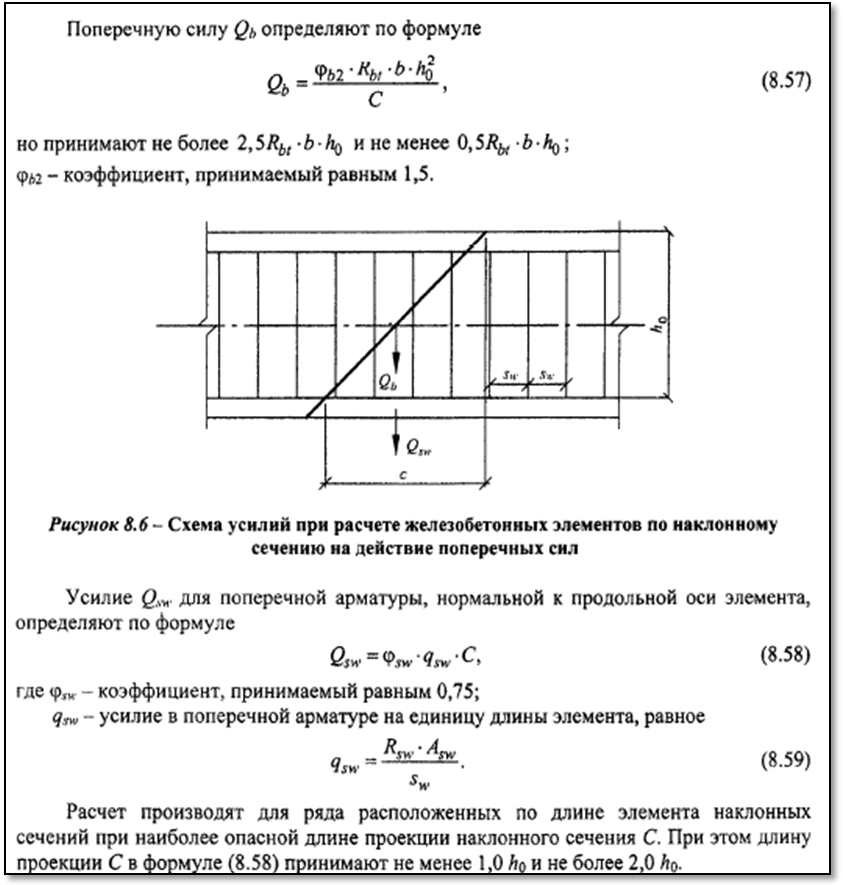
Расчеты с Формулой Поперечного Сечения: Изучение Площади
При анализе задач по сопротивлению материалов используются параметры, вводимые в расчетные формулы. Эти параметры определяют форму и размеры поперечных сечений и называются геометрическими характеристиками плоских сечений.
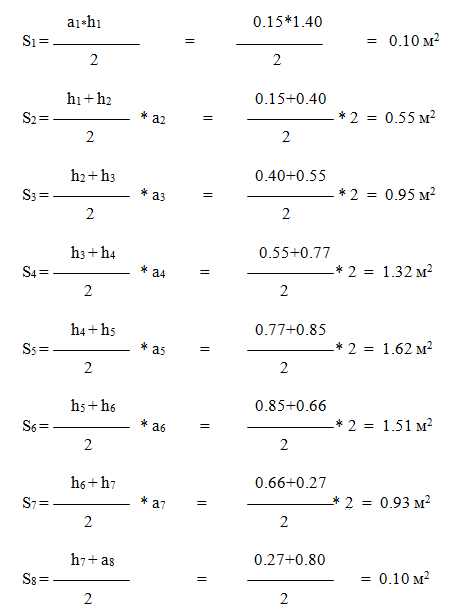
S = πR2
При этом не стоит забывать о том, что расстояние от плоскости до центра фигуры совпадет с плоскостью, тогда плоскость поперечного сечения шара будет равняться нулю, так как касание им плоскости происходит лишь в одной точке.
Рассмотрим на примере параллелограмма. Прежде всего, для того чтобы найти площадь поперечного сечения, необходимо знать значения высоты и снования параллелограмма. Даже если нам известна только ширина основания и его длина через эти значения возможно найти диагональ, используя теорему Пифагора: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Формула выглядит как:
a2 + b2 = c2
Из нее можно вывести такую формулу:
c = S*q*r*t*(a2 + b2)
Когда у нас известно значение диагонали параллелограмма, то его можно подставить в формулу:
S= c*h
S – площадь поперечного сечения, h это значений высоты параллелограмма. Результат, который получится после исчислений, будет означать площадь поперечного сечения. Такая формула:
S=a*b
используется в тех случаях, когда сечение идет параллельно двум основаниям.
При вычислении площади поперечного сечения цилиндра, которое проходит вдоль его оснований, если одна из сторон данного прямоугольника тождественна радиусу основания, а другая из сторон – высоте цилиндра используется такая формула:
S =2R*h
где h – высота цилиндра R – величина радиуса окружности. Если же сечение не проходит сквозь ось цилиндра и одновременно параллельно его основаниям, то это означает, что сторона данного треугольника не равняется диаметру окружности основания.
Для решения этой проблемы необходимо узнать значение неизвестной стороны предварительно нарисовав окружность у основания цилиндра. Расчет производится также по формуле выведенной из теоремы Пифагора. Затем подставляется формула:
S =2а*h
где 2а – значение хорды, расчета площади поперечного сечения.
Какие сечения проводов есть?
Сечение провода — это площадь проводника, который проходит электрический ток. Различные типы проводов имеют различные сечения, которые определяются их электрическими характеристиками, включая проводимость, напряжение и теплопроводность.
Некоторые из самых распространенных сечений проводов:
- Сечение провода в мм2: 0,5, 0,75, 1, 1,5, 2,25, 4, 6, 10, 16, 25, 35, 50, 70, 95, 120, 150 и т.д.
- Сечение провода в AWG (American Wire Gauge): 20, 18, 16, 14, 12, 10, 8 и т.д.
Выбор сечения провода зависит от многих факторов, включая мощность электрической нагрузки, длину провода и электрические характеристики провода. Важно выбрать правильное сечение провода, чтобы избежать перегрева или перегрузки электрической системы.