Онлайн-калькулятор для расчета металлических ферм из профильной трубы на SolidIron.ru
- Строительные калькуляторы — ProstoBuild.ru
- Расчет металлической фермы
- Расчет фермы онлайн калькулятор
Строительные калькуляторы — ProstoBuild.ru
В некоторых случаях нам не удается использовать обычную балку для определенных конструкций, поэтому приходится прибегать к более сложной форме — металлической ферме. Этот метод отличается от расчета обычной балки, однако рассчитать ферму для нас не составит труда. Если нужно, мы можем воспользоваться онлайн-калькулятором для расчета металлических ферм из профильной трубы.
Расчет металлической фермы хоть и отличается от расчета балки, но нам не составит труда ее рассчитать. От вас будет требоваться лишь внимание, начальные знания алгебры и геометрии и час-два свободного времени.
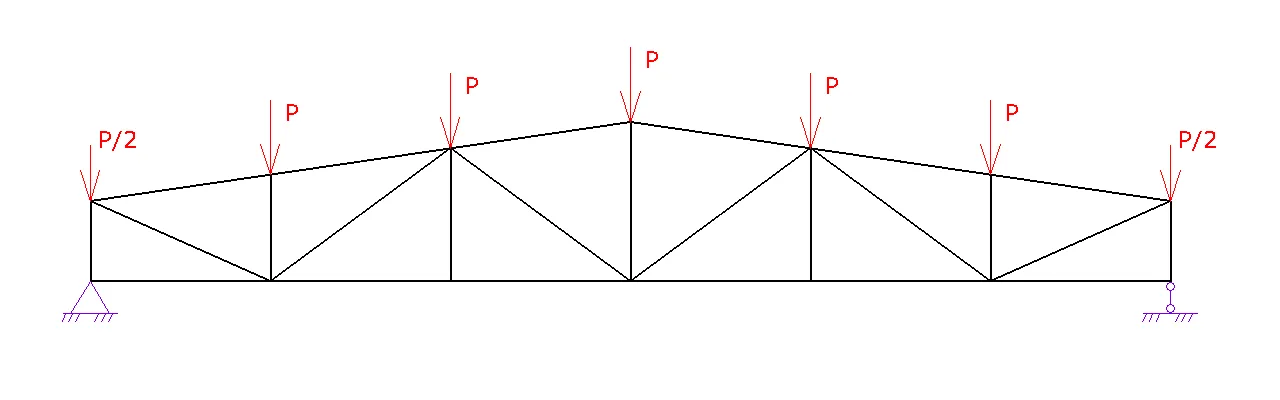
Итак, начнем. Перед тем, как рассчитывать ферму, давайте зададимся какой-нибудь реальной ситуацией, с которой вы бы могли столкнуться. Например, вам необходимо перекрыть гараж шириной 6 метров и длиной 9 метров, но ни плит перекрытия, ни балок у вас нету. Только металлические уголки различных профилей. Вот из них мы и будем собирать нашу ферму!
В последующем на ферму будут опираться прогоны и профнастил. Опирание фермы на стены гаража – шарнирное.
Для начала вам необходимо будет узнать все геометрические размеры и углы вашей фермы. Здесь нам и понадобится наша математика, а именно — геометрия. Углы находим при помощи теоремы косинусов.
Затем нужно собрать все нагрузки на вашу ферму (посмотреть можно в статье Расчет навеса). Пусть у вас получился следующий вариант загружения:
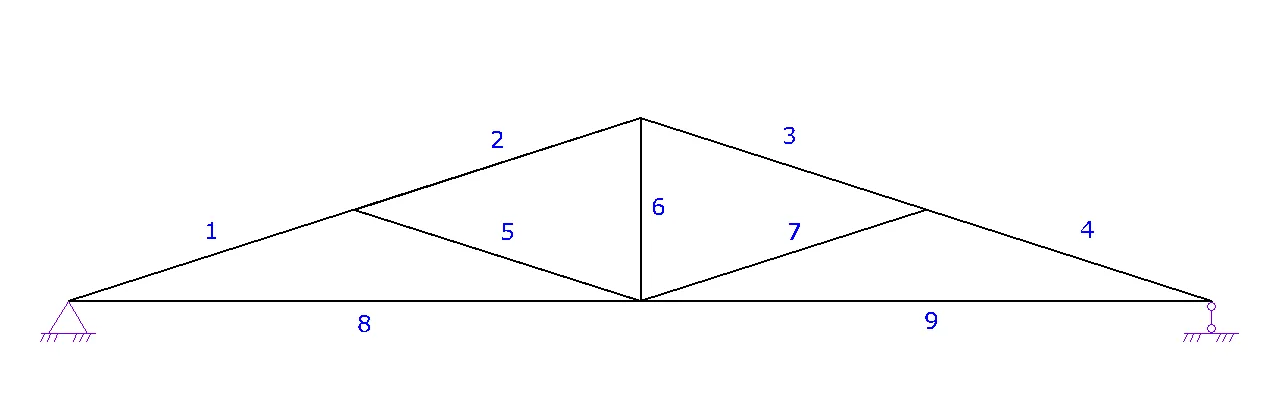
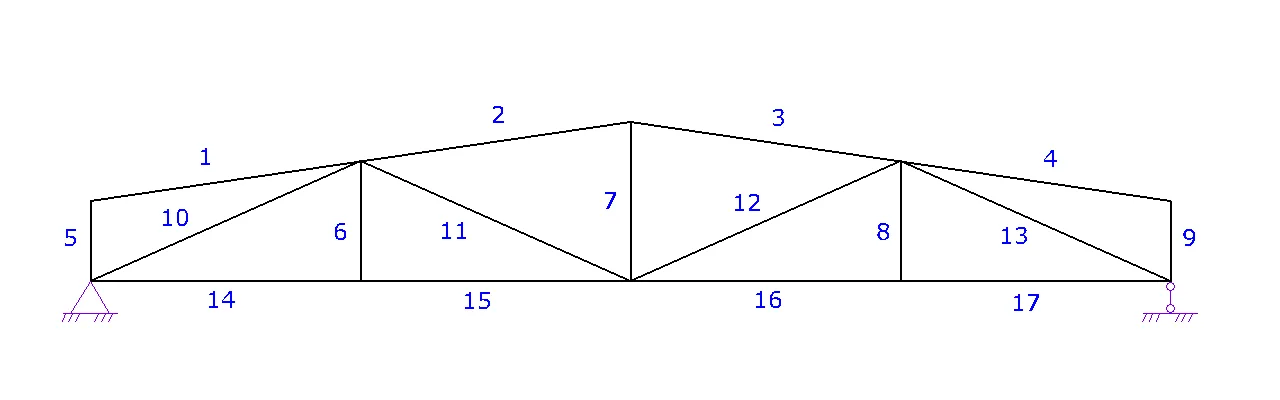
Далее нам нужно пронумеровать все элементы, узлы фермы и задать опорные реакции (элементы подписаны зеленым, а узлы голубым).
Чтобы найти наши реакции, запишем уравнения равновесия усилий на ось y и уравнение равновесия моментов относительно узла 2.
Из второго уравнения находим опорную реакцию Rb:
Зная, что Rb=400 кг, из 1-ого уравнения находим Ra:
После того, как опорные реакции известны, мы должны найти узел, где меньше всего неизвестных величин (каждый пронумерованный элемент — это неизвестная величина). С этого момента мы начинаем разделять ферму на отдельные узлы и находить внутренние усилия стержней фермы в каждом из этих узлов. Именно по этим внутренним усилиям мы и будем подбирать сечения наших стержней.
Если получилось так, что усилия в стержне направлены от центра, значит наш стержень стремится растянуться (вернуться в первоначальное положение), а значит сам он сжат. А если усилия стержня направлены к центру, значит стержень стремится сжаться, то есть он растянут.
Итак, перейдем к расчету. В узле 1 всего 2 неизвестных величины, поэтому рассмотрим этот узел (направления усилий S1 и S2 задаем из своих соображений, в любом случае у нас по итогу получится правильно).
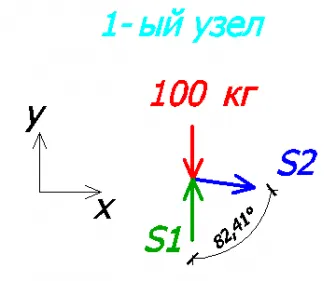
Рассмотрим уравнения равновесия на оси х и у.
Из 1-ого уравнения видно, что S2=0, то есть 2-ой стержень у нас не загружен!
Из 2-ого уравнения видно, что S1=100 кг.
Поскольку значение S1 у нас получилось положительным, значит направление усилия мы выбрали правильно! Если же оно бы получилось отрицательным, то направление стоит поменять и знак изменить на «+».
Зная направление усилия S1, мы можем представить, что из себя представляет 1-ый стержень.
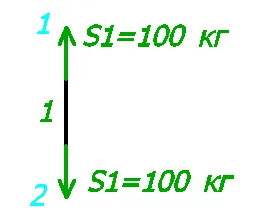
Поскольку одно усилие было направлено в узел (узел 1), то и второе усилие будет направлено в узел (узел 2). Значит наш стержень старается растянуться, а значит он сжат.
Далее рассмотрим узел 2. В нем было 3 неизвестных величины, но поскольку мы уже нашли значение и направление S1, то остается только 2 неизвестных величины.

Опять же составим уравнения на оси х и у:
Из 1-ого уравнения S3 = 540,83 кг (стержень №3 сжат).
Из 2-ого уравнения S4 = 450 кг (стержень №4 растянут).

Составим уравнения на оси х и у:

Составим уравнения на оси х и у:
ИЗ 1-ого уравнения находим S12:
Из 2-ого уравнения находим S10:
Дальше рассмотрим узел №3. Насколько мы помним 2-ой стержень у нас нулевой, а значит рисовать его не будем.

А здесь нам уже понадобится алгебра. Я не буду подробно расписывать методику нахождения неизвестных величин, но суть такова – из 1-ого уравнения выражаем S5 и подставляем ее во 2-ое уравнение.
Составим уравнения на оси х и у:
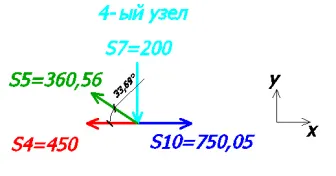
Так же, как и в 3-ем узле найдем наши неизвестные.

Из 1-ого уравнения находим S7:
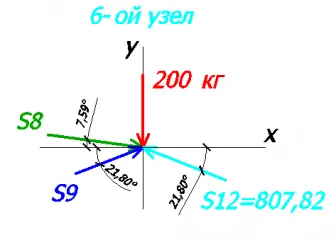
В качестве проверки наших расчетов рассмотрим 4-ый узел (усилий в стержне №9 нету):
Составим уравнения на оси х и у:
В 1-ом уравнении получается:
Данная погрешность допустима и связана скорее всего с углами (2 знака после запятой вместо 3-ех).
По итогу у нас получатся следующие значения:
Решил перепроверить все наши расчеты в программе и получил точно такие же значения:

При расчете металлической фермы после того, как все внутренние усилия в стержнях найдены, мы можем приступать к подбору сечения наших стержней.
Для удобства все значения сведем в таблицу.
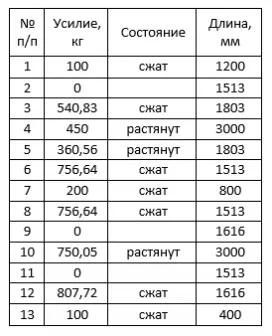
Для расчетов нам понадобится не фактическая длина, а расчетная. Расчетную длину мы сможем найти в СНиП II-23-81* «Стальные конструкции». Таблица приведена ниже:

Как видно из таблицы, мы будем проверять стержень фермы в двух направлениях:
— из плоскости фермы (перпендикулярно плоскости фермы)
Чтобы найти расчетную длину стержня из плоскости фермы, нам нужно посмотреть, через какое расстояние этот стержень раскреплен с другой фермой. Например, по верхнему поясу наша ферма раскреплена связью/прогоном с другой фермой по центру. Значит расчетная длина верхнего пояса равна половине его длины. Если же верхний пояс раскреплен из плоскости в каждом узле, то расчетная длина стержня из плоскости такая же, как и в плоскости, и равна значениям в таблице выше.
Дальше, в зависимости от того сжат стержень или нет, по формуле мы рассчитываем необходимую площадь поперечного сечения.
При расчете сжатых стержней мы пользуемся формулой (необходимая площадь стержня):
По данной формуле можно рассчитать в этом онлайн расчете.
А также проверяем наш стержень на максимальную гибкость. Как правило, максимальная гибкость не должна быть больше 100-150.
Где lx – расчетная длина в плоскости фермы
Ly – расчетная длина из плоскости фермы
Ix – радиус инерции сечения вдоль оси х
Iy – радиус инерции сечения вдоль оси у
При расчете растянутых стержней мы пользуемся следующей формулой (необходимая площадь стержня):
Данной формулой можно воспользоваться в онлайн расчете растянутых элементов.
Например, два спаренных уголка 32х3 выдержат усилие равное 3.916*2 = 7,832 т.
Источник
Расчет фермы онлайн калькулятор
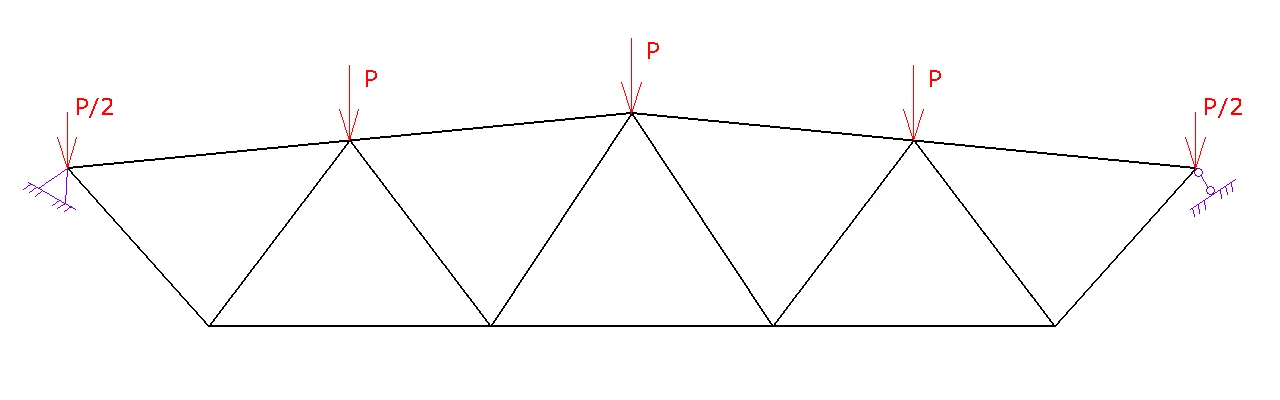
При строительстве или проектировании навеса или кровли в качестве несущего элемента часто используется ферма, но мало кто знает, какие задать сечения стержней и рационально ли применять данное сечение. На эти вопросы Вам поможет ответить данный калькулятор фермы.
Ферма может быть как деревянной, так и металлической. В этом калькуляторе представлены два этих материала на Ваш выбор. Их обязательно нужно выбрать на 4 шаге!
При выборе металлической фермы среди сечений можно найти профильные квадратные и прямоугольные трубы, уголок и различные его сечения, швеллер и круглые трубы. При выборе деревянной фермы – круг, квадрат и прямоугольник.
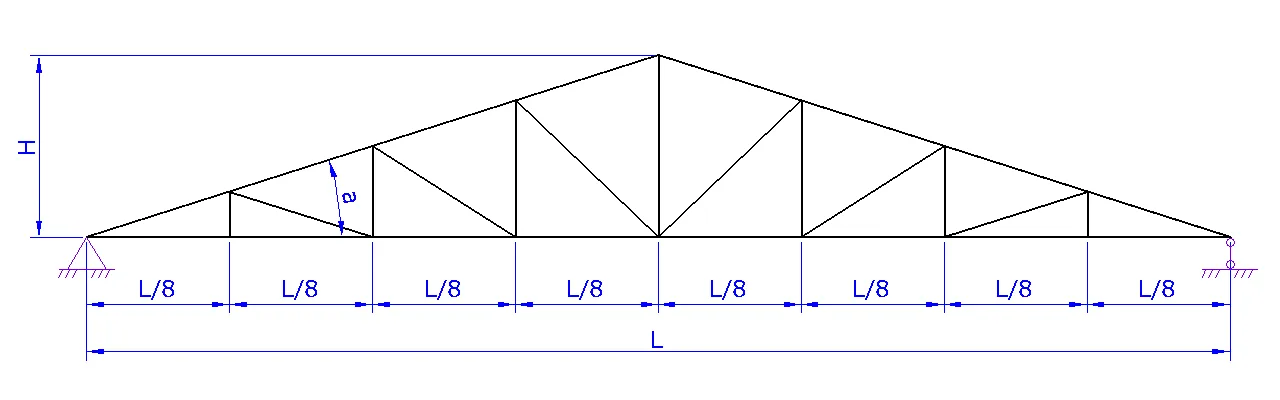
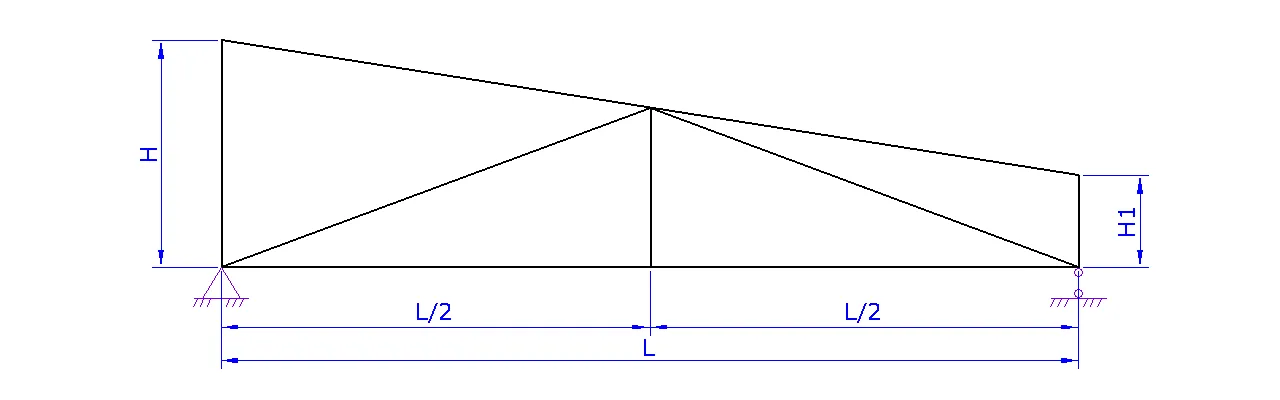
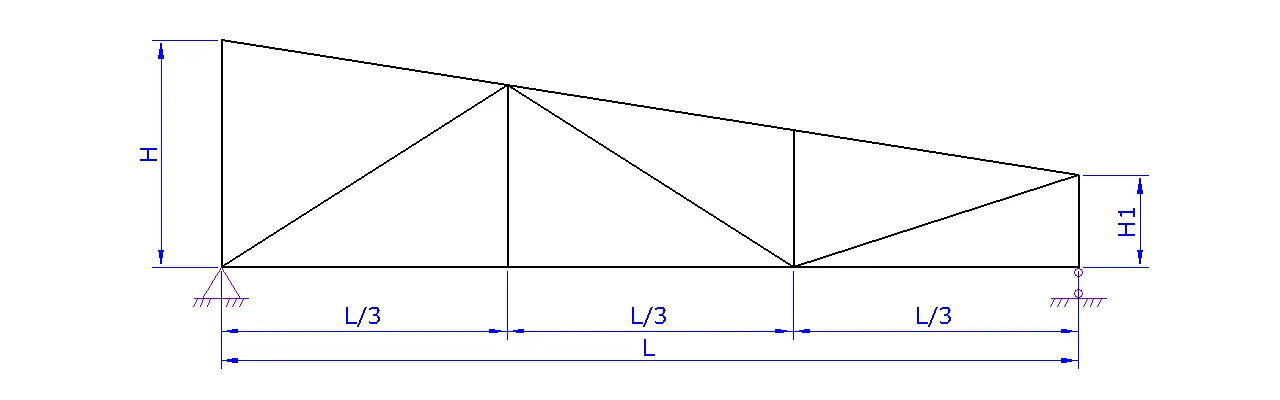
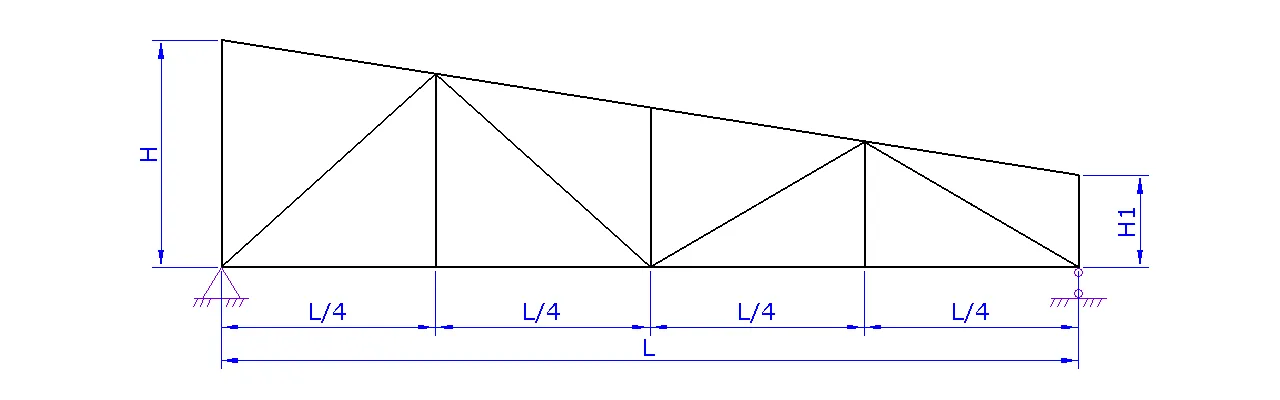





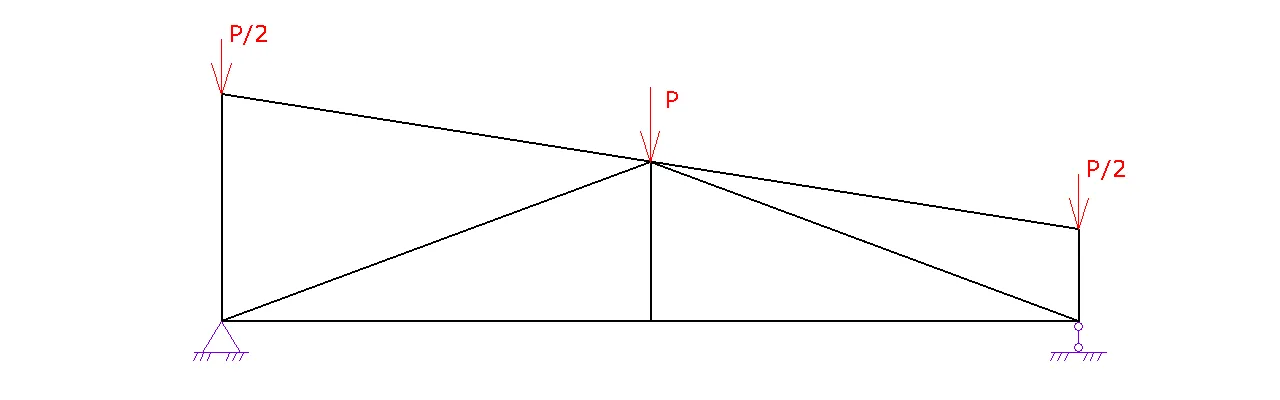
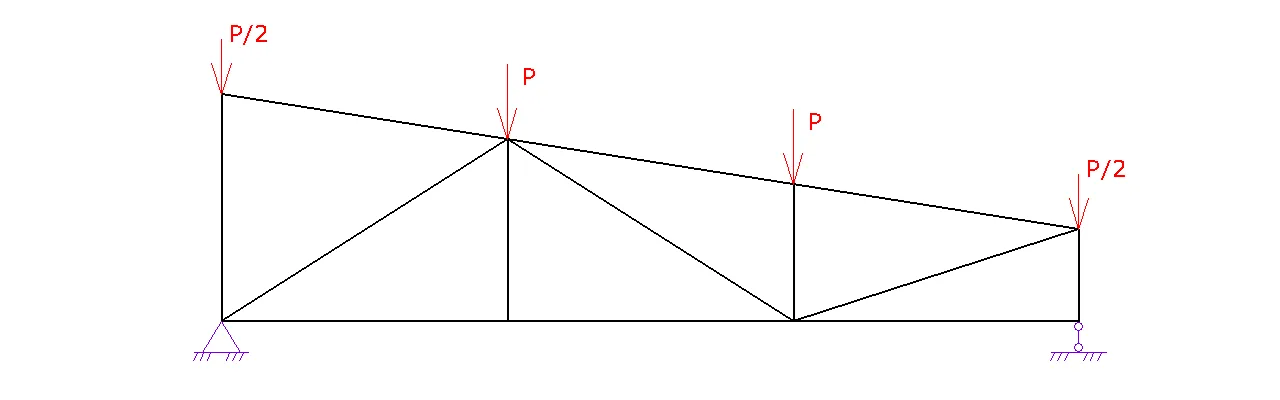

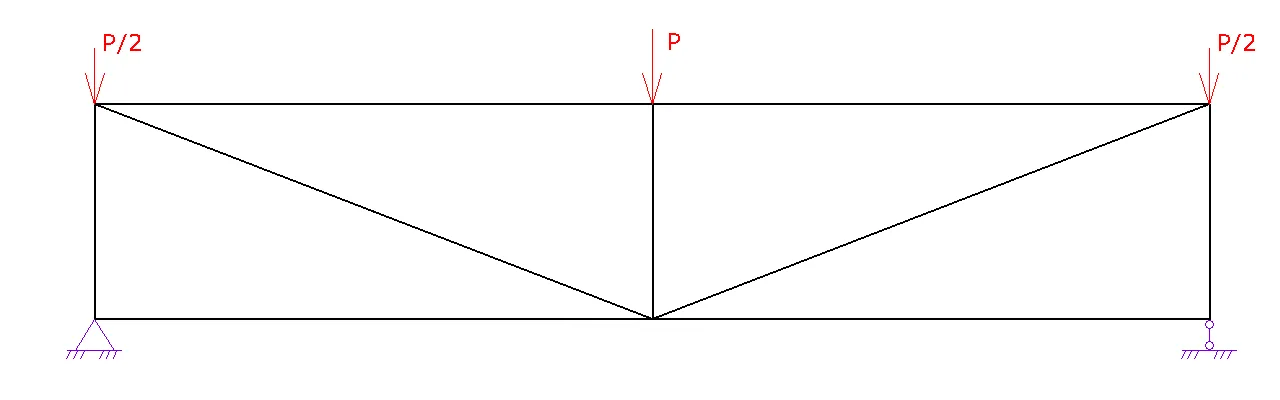
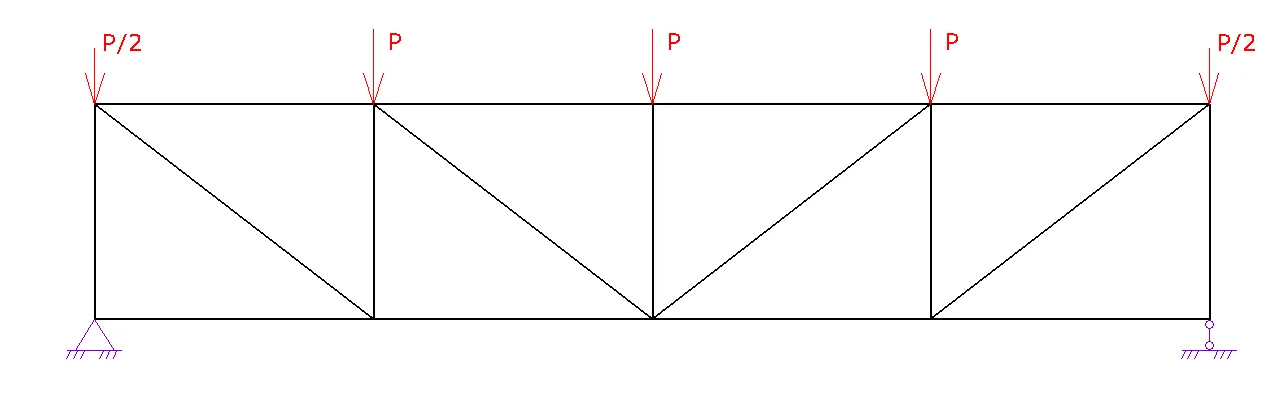















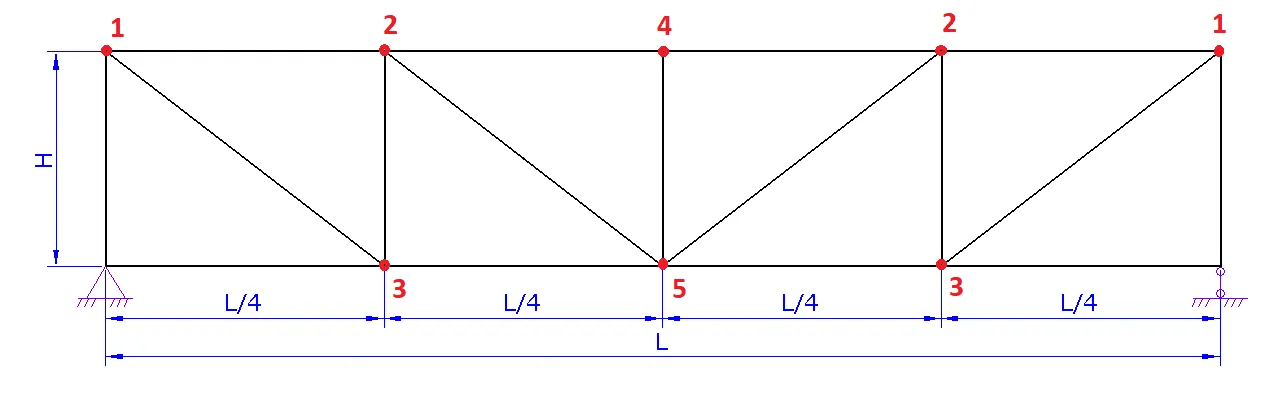


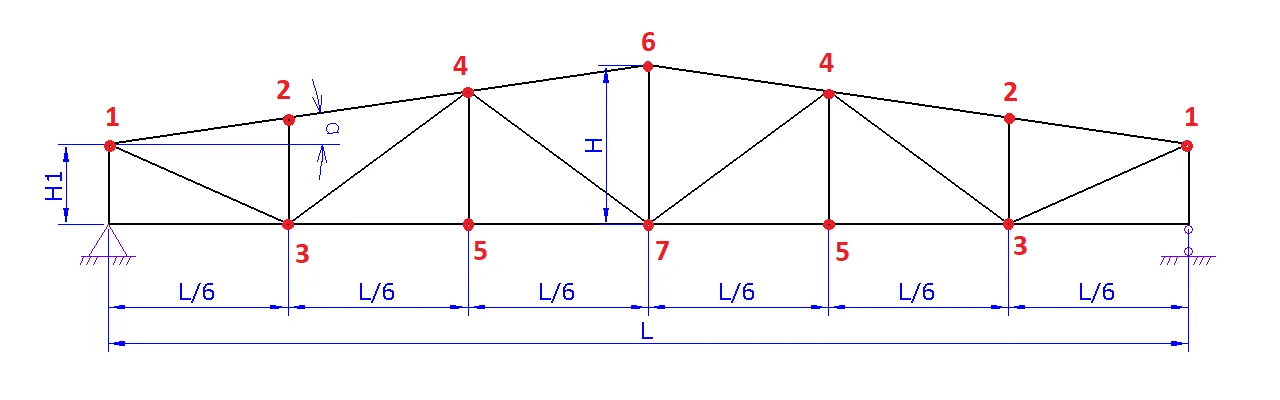


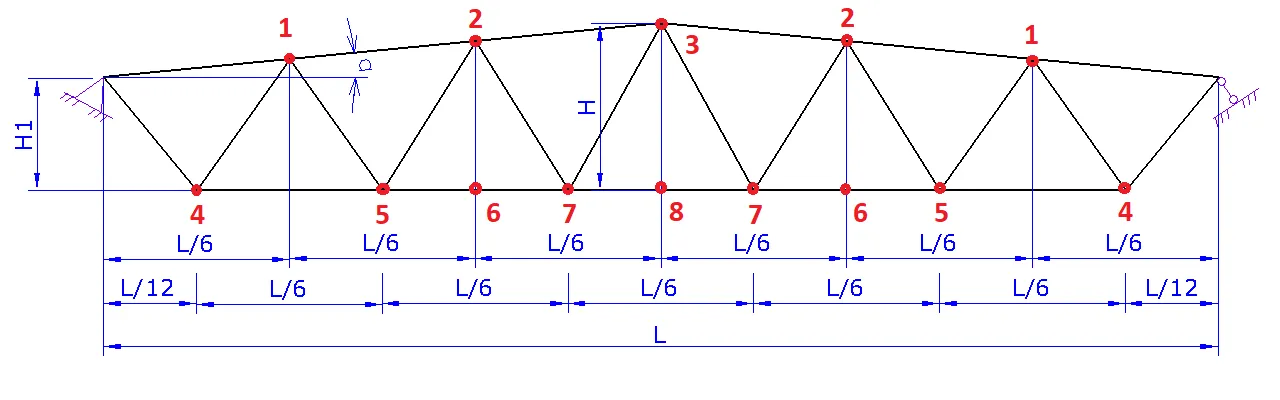
















Расчет фермы
> +> +> +> +> +> +> +> +> +> +> +> +> +> +> +> +> +> +> +> +> +> +> +> +> +> +> +> +=’2′ || x2 >=’1′ || x3 >=’1′ || x4 >=’1′ || x5 >=’1′»> =’2′ || x2 >=’1′ || x3 >=’1′ || x4 >=’1′ || x5 >=’1′»> =’3′ || x2 >=’2′ || x3 >=’2′ || x4 >=’1′ || x5 >=’1′»> =’3′ || x2 >=’2′ || x3 >=’2′ || x4 >=’1′ || x5 >=’1′»> =’4′ || x2 >=’3′ || x3 >=’2′ || x4 >=’1′ || x5 >=’1′»> =’4′ || x2 >=’3′ || x3 >=’2′ || x4 >=’1′ || x5 >=’2′»> =’4′ || x3 >=’3′ || x4 >=’2′ || x5 >=’2′»> =’4′ || x3 >=’3′ || x4 >=’2′ || x5 >=’2′»> =’5′ || x3 >=’3′ || x4 >=’2′ || x5 >=’2′»> =’5′ || x3 >=’3′ || x4 >=’2′»> =’5′ || x4 >=’3′»> =’5′ || x4 >=’3′»> =’3′»> =’3′»>
| № | Расч. усилия, кг | Сечение | Запас, % | Гибкость |
|---|---|---|---|---|
| 1 | <> | =’1′» >- <> + | <> | <> ? |
| 2 | <> | =’1′» >- <> + | <> | <> ? |
| 3 | <> | =’1′» >- <> + | <> | <> ? |
| 4 | <> | =’1′» >- <> + | <> | <> ? |
| 5 | <> | =’1′» >- <> + | <> | <> ? |
| 7 | <> | =’1′» >- | <> | <> ? |
| 9 | <> | =’1′» >- | <> | <> ? |
| 11 | <> | =’1′» >- | <> | <> ? |
| 13 | <> | =’1′» >- | <> | <> ? |
| 15 | <> | =’1′» >- | <> | <> ? |
| 17 | <> | =’1′» >- | <> | <> ? |
| 19 | <> | =’1′» >- | <> | <> ? |
| 21 | <> | =’1′» >- | <> | <> ? |
| 23 | <> | =’1′» >- | <> | <> ? |
| 25 | <> | =’1′» >- | <> | <> ? |
| 27 | <> | =’1′» >- | <> | <> ? |
| 29 | <> | =’1′» >- | <> | <> ? |
| 31 | <> | =’1′» >- | <> | <> ? |
| 33 | <> | =’1′» >- | <> | <> ? |
| Ориентировочная масса фермы | <> | кг |
<<<<<<<<<<<<<<<<<<<<<<<<<<<<
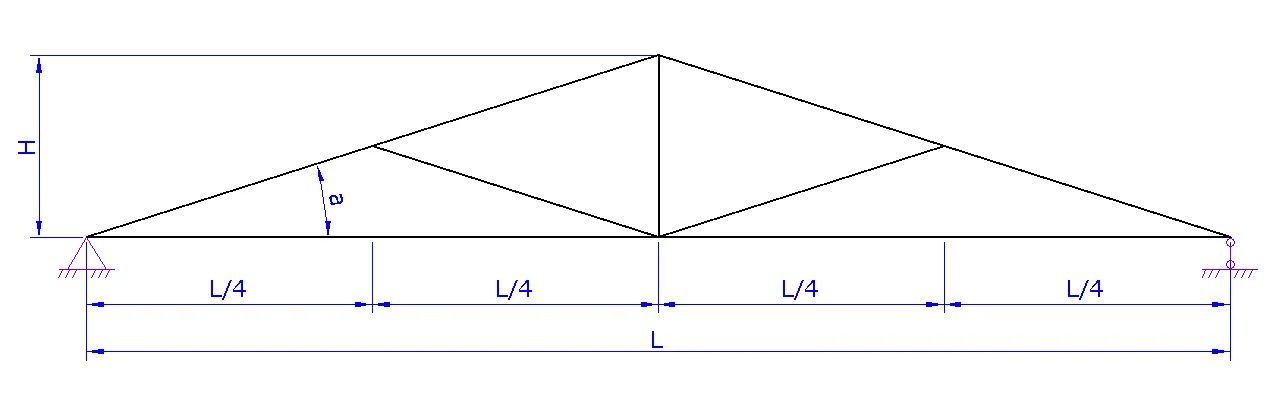
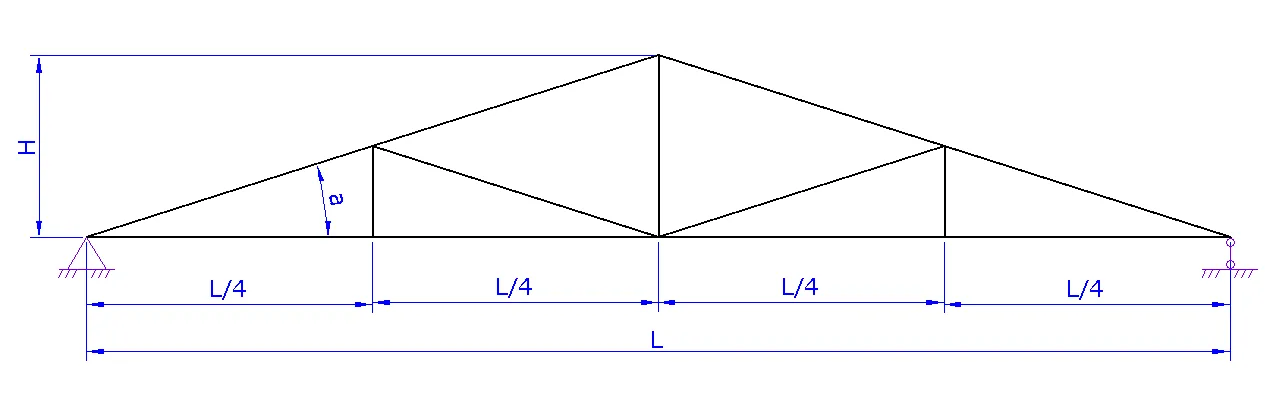
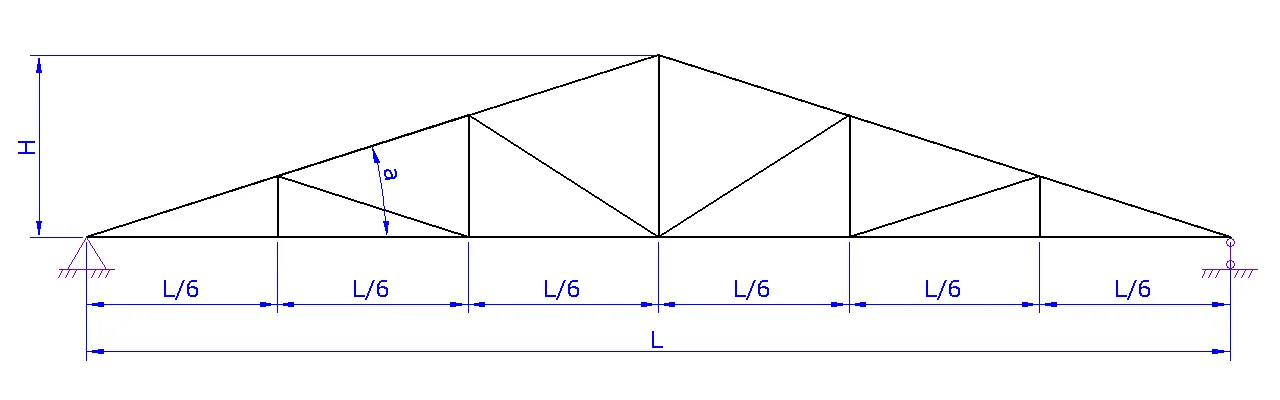
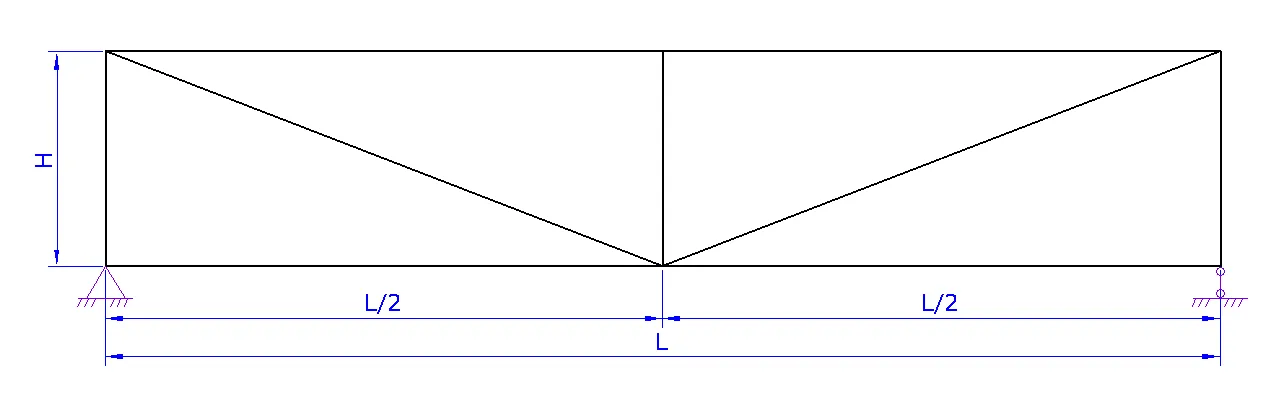
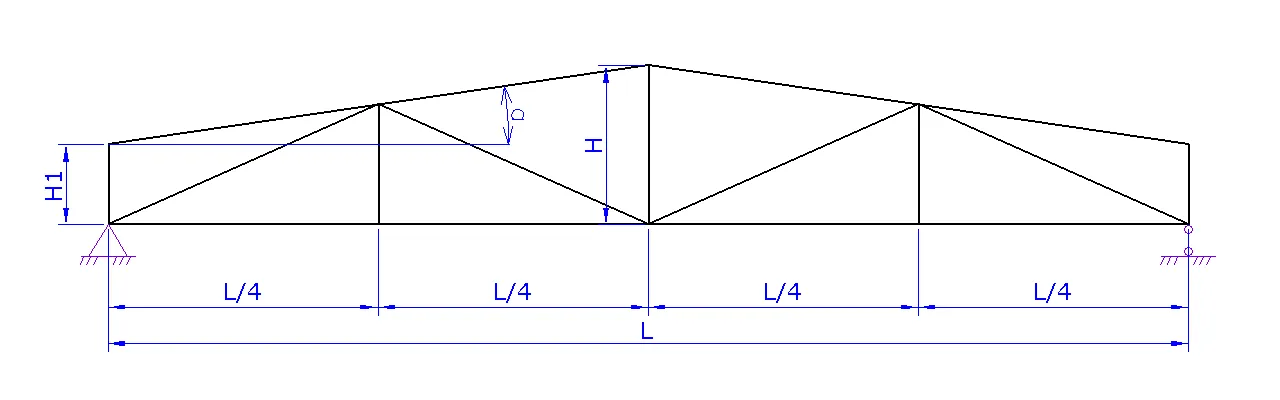
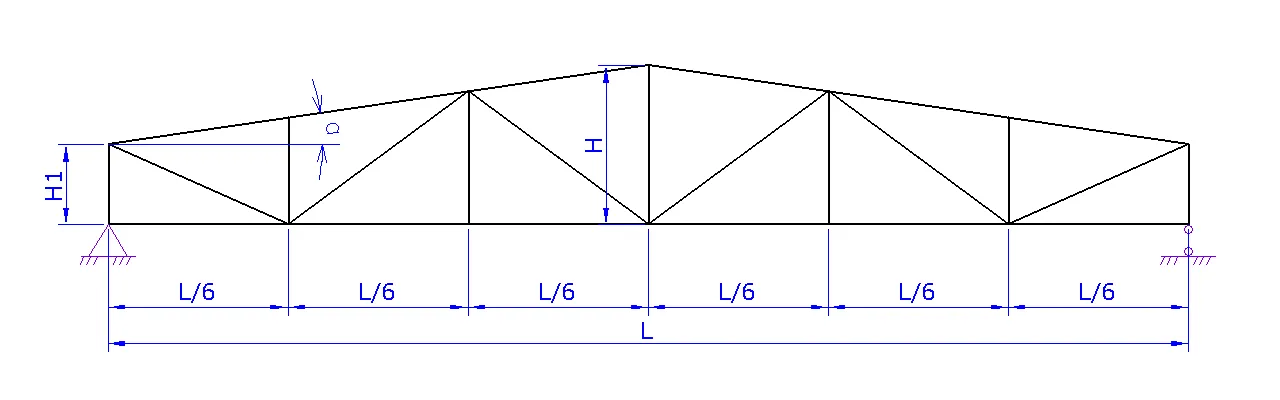
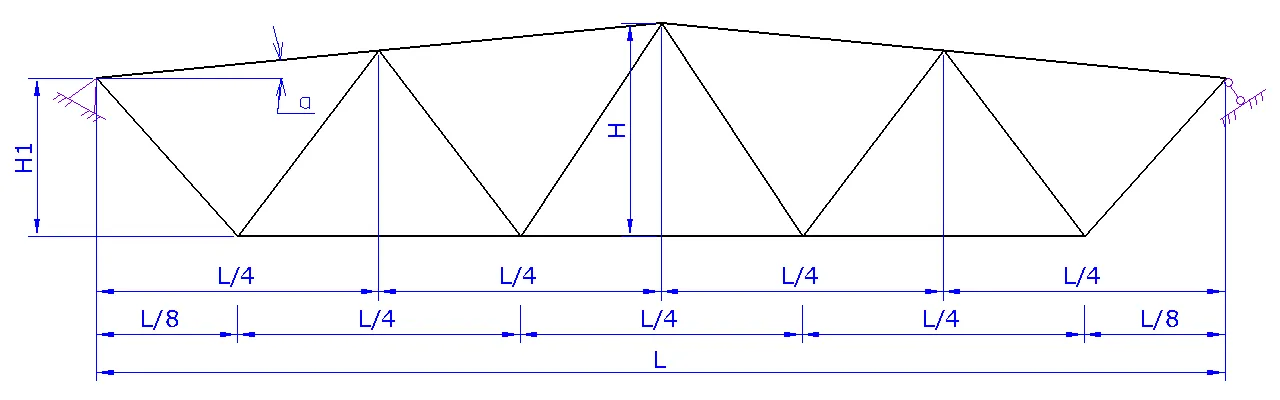
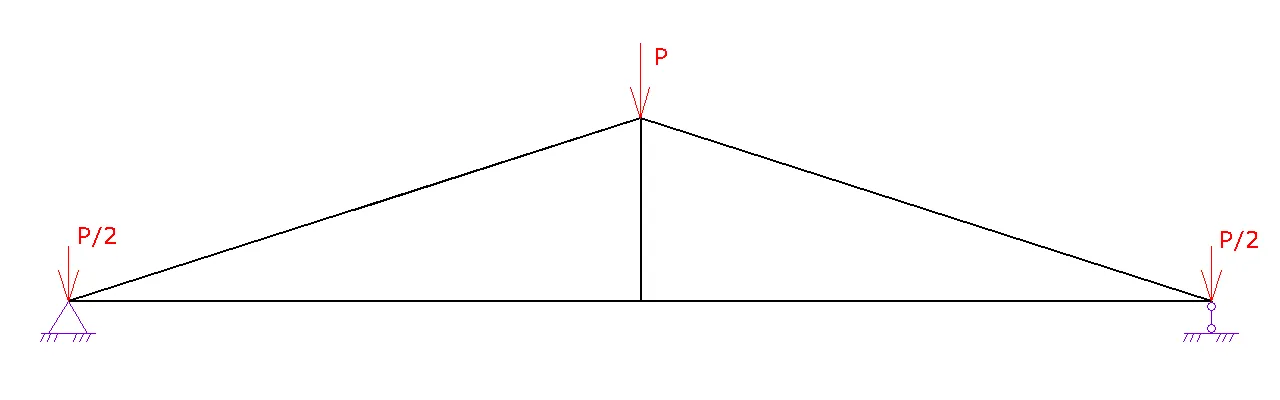
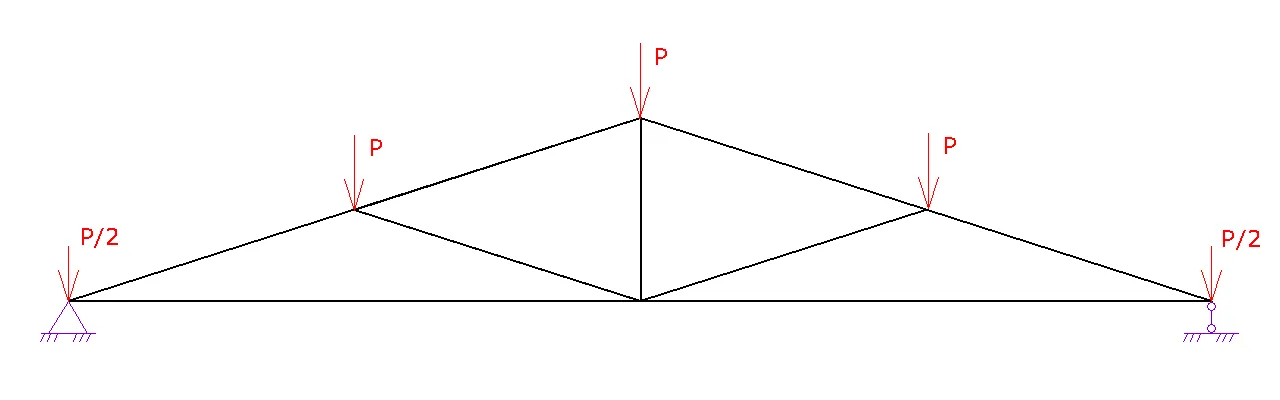
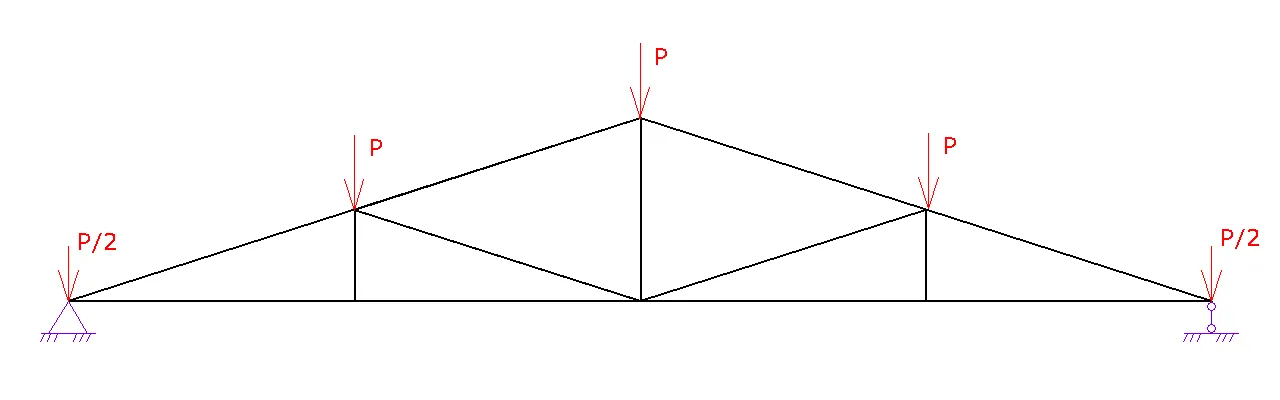
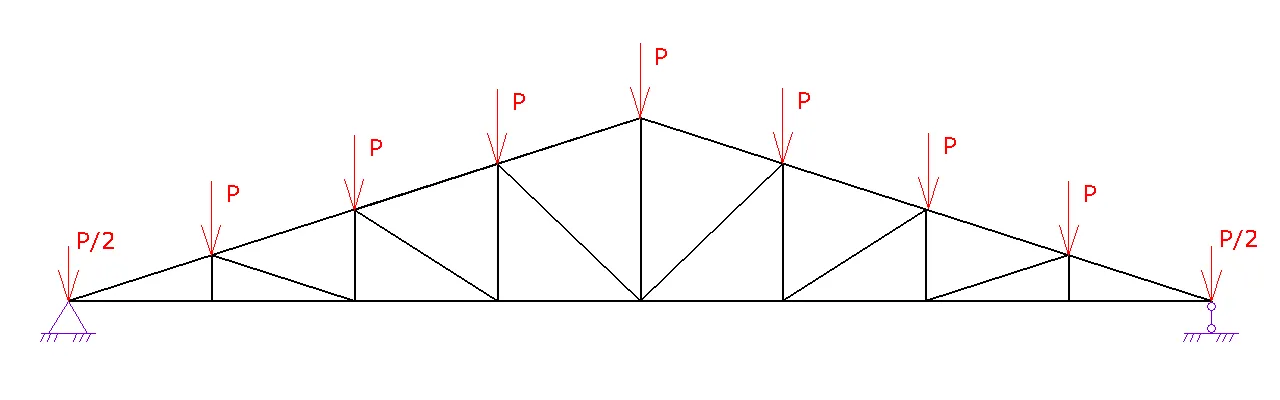
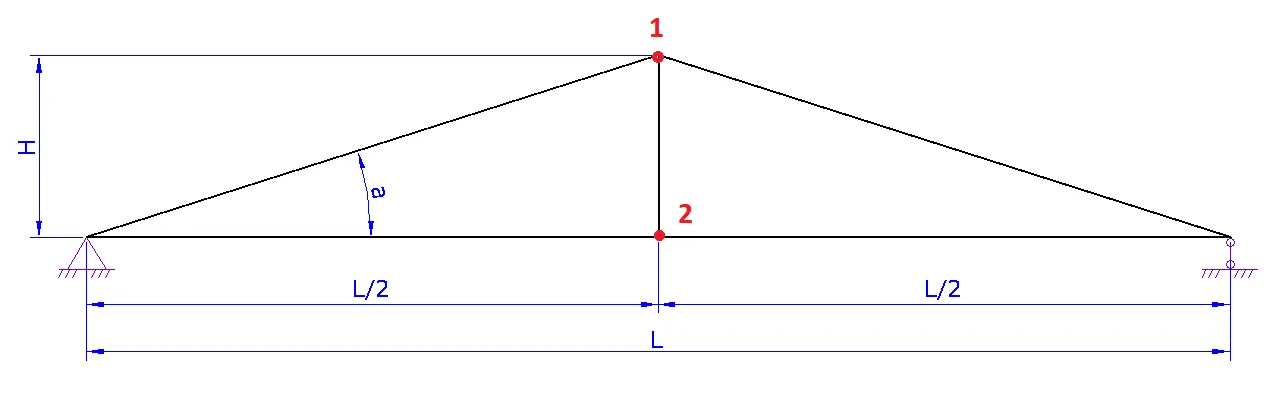
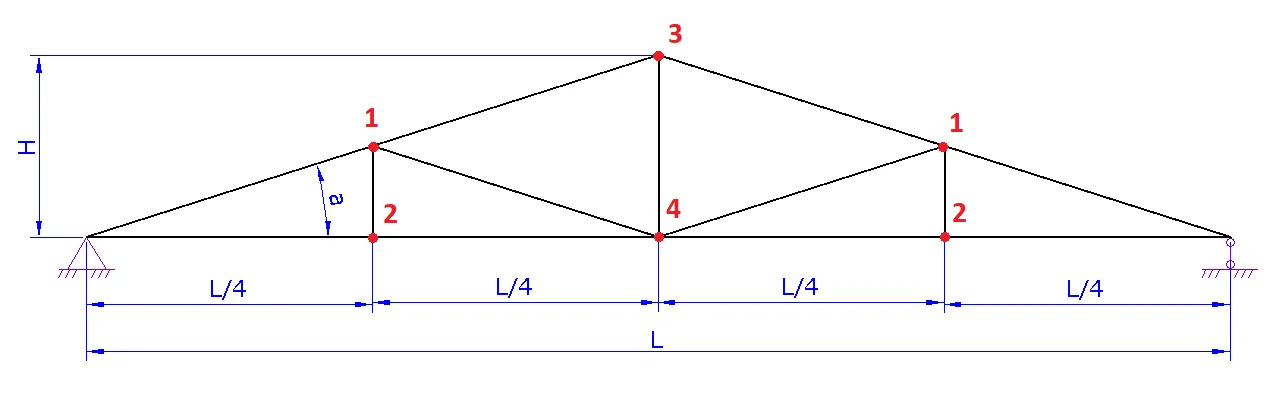
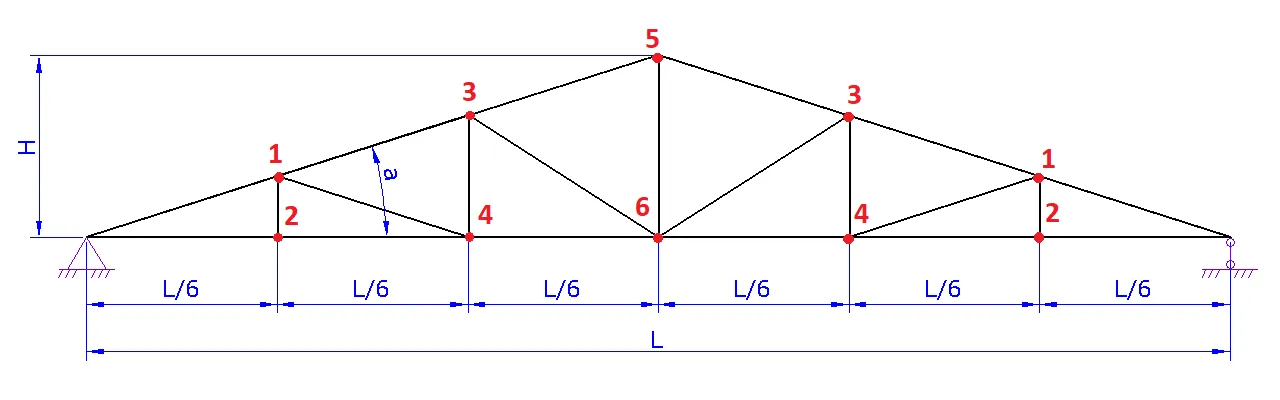
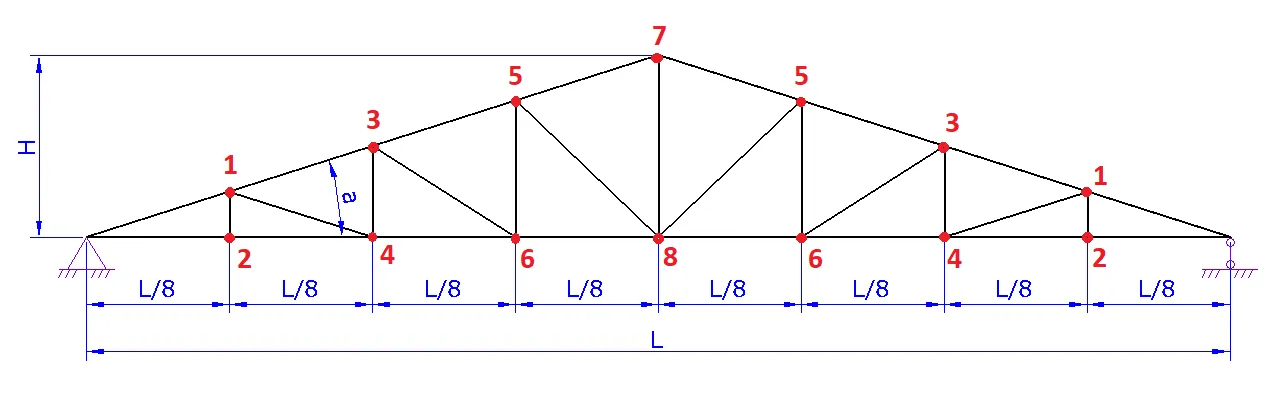
1. Шаг 1. Вид фермы. Выберите необходимый вид вашей фермы и нажмите на следующий шаг
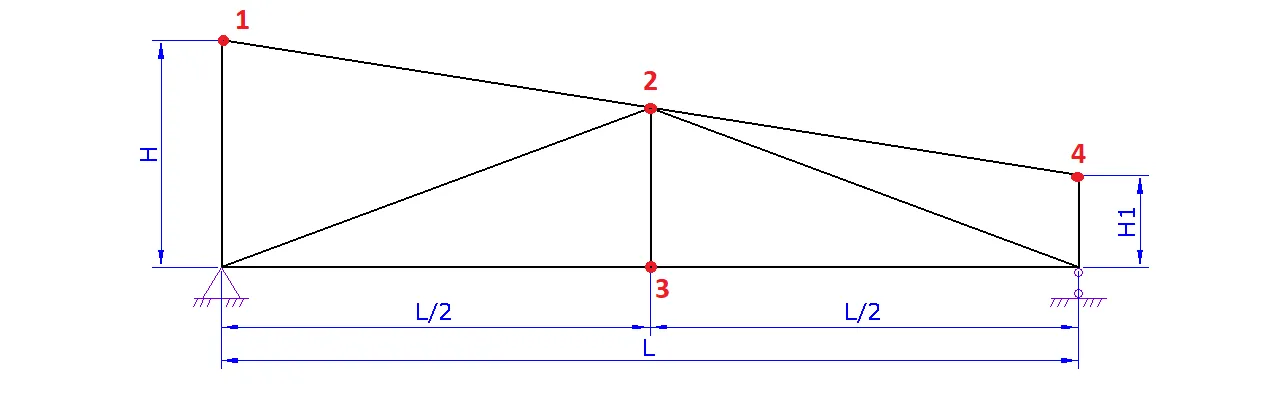
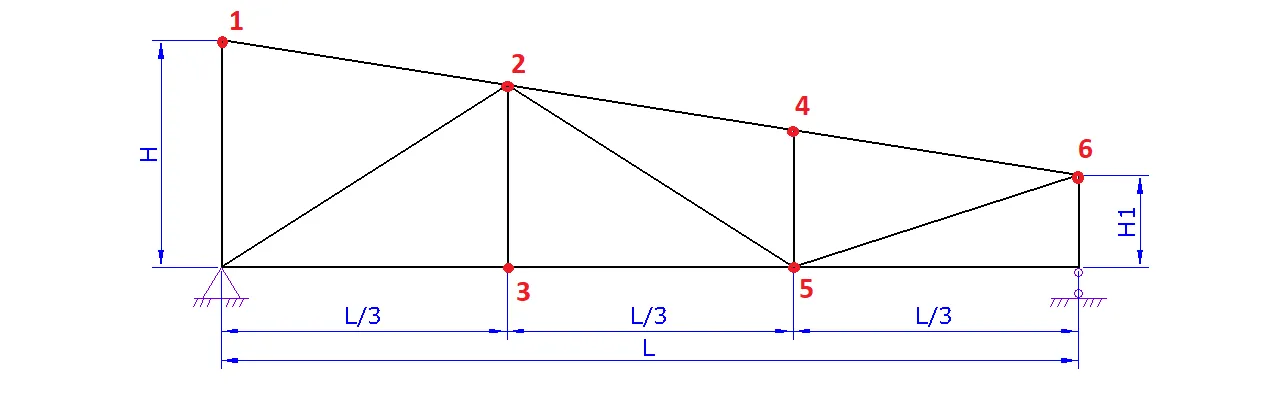
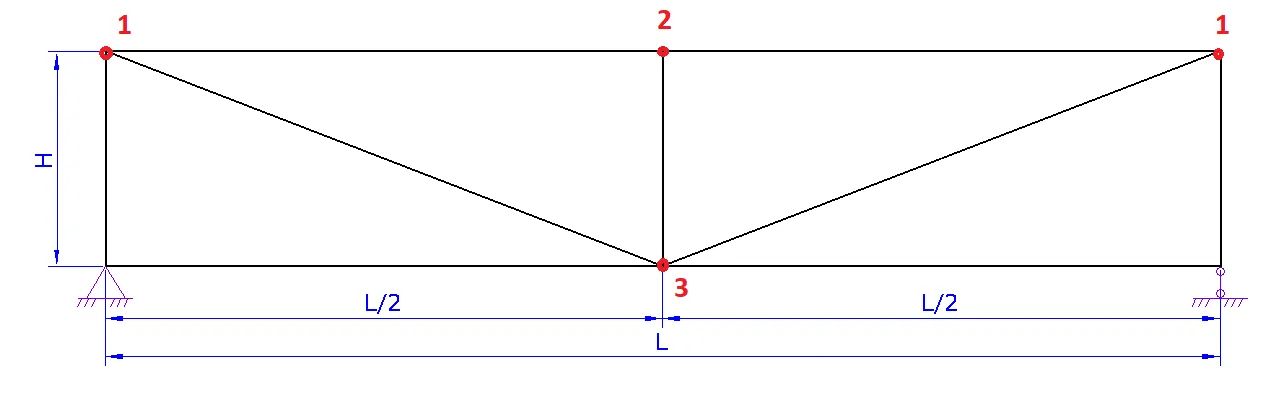
2. Шаг 2. Геометрия фермы.
a. Задайте схему фермы. В данном шаге можно поменять расположение стоек и раскосов для разных длин ферм
b. Задайте пролет фермы L
c. Задайте высоту фермы H либо угол а
d. При необходимости надо задать высоту фермы на опоре H1
e. Нажать на следующий шаг
3. Шаг 3. Нагрузки на ферму. Задайте сосредоточенную нагрузку на узлы фермы и нажмите на следующий шаг либо выберите «Задать нагрузку на площадь» и задайте распределенную нагрузку на 1м2 и шаг между фермами. Сосредоточенная нагрузка P на узел при этом пересчитается.
4. Шаг 4. Сечение и материал фермы.
a. Задайте материал фермы: сталь или дерево
b. Задайте сечение элементов фермы и класс/сорт материала данных элементов (при необходимости можете нажать на кнопку «для всех » и сечение/класс/сорт в 1-ой строке будет продублирован для всех строк)
c. Нажать на следующий шаг
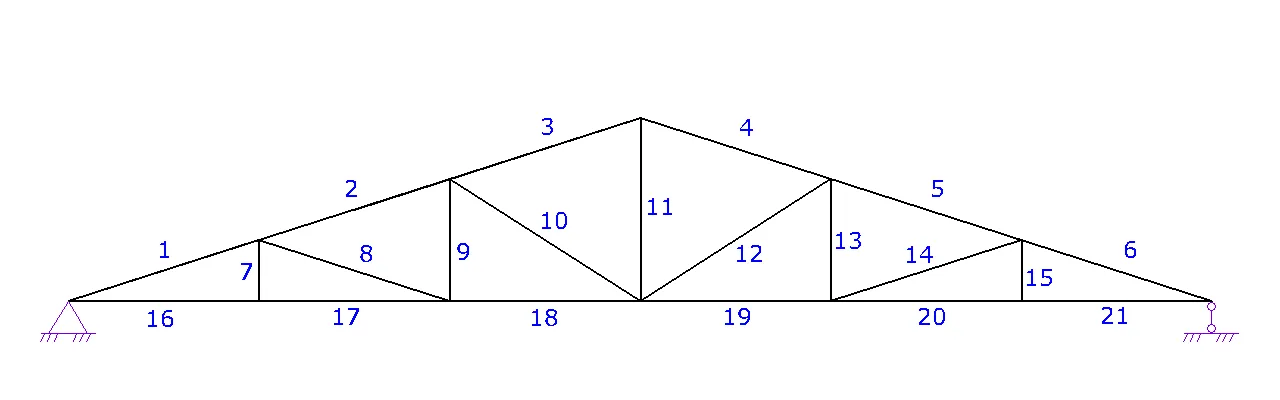
5. Шаг 5. Связи. Согласно рисунку расставить точки раскрепления узлов из плоскости фермы. Раскреплением из плоскости может служить как связь между фермами, так и прогоны

На рисунке видно, что узлы №1 и №3 из плоскости раскреплены прогонами (голубые), узлы №2 раскреплены горизонтальными связями по нижнему поясу (коричневые), а узел №4 ничем не раскреплен
6. Шаг 6. Результат расчета. Нажать на кнопку «Расчет»
Все полученные значения будут сведены в таблицу ниже, в которой вы сможете узнать следующие значения:
1. Расчетные усилия в стержнях фермы (если стержень сжат – значение отрицательное, если стержень растянут – положительное, если значение равно нулю – значит, это нулевой стержень и сечение принимайте конструктивно)
2. Сечение стержней фермы. Рядом с каждым сечением будут кнопки « — » и « + », которыми можно уменьшать либо увеличивать сечение стержня.
3. Запас по прочности/устойчивости (расчет считает с минимальным запасом в 50%). Если запас подсвечен красным и равен нулю – принимать такое сечение нельзя, и надо либо менять схему фермы, либо задавать другое сечение.
4. Гибкость стержня. Немаловажный параметр, который также ограничивает принимаемые сечения стержней фермы. Если гибкость равна «NO» или подсвечена красным – принимать такое сечение нельзя, и надо либо менять схему фермы, либо задавать другое сечение.
5. Ориентировочная масса фермы. При расчете данной величины учтите, что сечение стержней фермы предварительно надо унифицировать (привести к схожим сечениям стержней)
Для справки:
— плотность дерева принята 500 кг/м3
— плотность стали — 7850 кг/м3
— все узлы фермы шарнирные
— опоры фермы – шарнирно неподвижная слева и шарнирно подвижная справа
Если данный калькулятор фермы оказался Вам полезен – не забывайте делиться им с друзьями и коллегами ссылкой в соц.сети, а также посмотреть другие строительные калькуляторы онлайн, они простые, но здорово облегчают жизнь строителям и тем, кто решил сам строить свой дом с нуля.
— Добавлена проверка растянутого и нулевого элемента стержня по гибкости
— Добавлена возможность раскрепления узлов фермы из плоскости
2. Добавлена возможность ввода распределенной нагрузки на 1м2
— Добавлена возможность задать точки раскрепления с определенным шагом
Источник
Как рассчитать профильную трубу на изгиб?
Для расчета профильной трубы на изгиб необходимо знать следующие параметры:
- Радиус изгиба (R) — это расстояние от оси изгиба до наружной поверхности трубы.
- Толщина стенки трубы (t).
- Длина отрезка трубы (L) между точками начала и конца изгиба.
- Угол изгиба (α) — это угол между линиями, проходящими через ось изгиба и касательную к наружной поверхности трубы в точке начала и конца изгиба соответственно.
Для расчета профильной трубы на изгиб можно использовать следующую формулу:
L = π * R * (α/180) + 2 * ((t/2) / tan(α/2))
где π — это число «пи» (округленное до 3,14)
Эта формула позволяет определить длину отрезка трубы (L), необходимого для создания изгиба с заданными параметрами.
Пример: Допустим, у нас есть профильная труба с толщиной стенки 3 мм и радиусом изгиба 50 мм. Нам нужно изготовить из этой трубы отрезок длиной 500 мм с углом изгиба 45 градусов. Как рассчитать необходимую длину отрезка трубы?
L = π * 50 мм * (45/180) + 2 * ((3 мм / 2) / tan(45/2)) L = 78,54 мм + 1,51 мм L = 80,05 мм
Таким образом, для изготовления отрезка профильной трубы длиной 500 мм с углом изгиба 45 градусов необходимо использовать трубу длиной 580,05 мм.